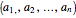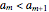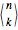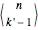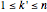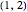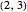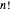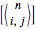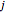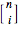Eulerian Numbers versus Stirling Numbers of the First Kind

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
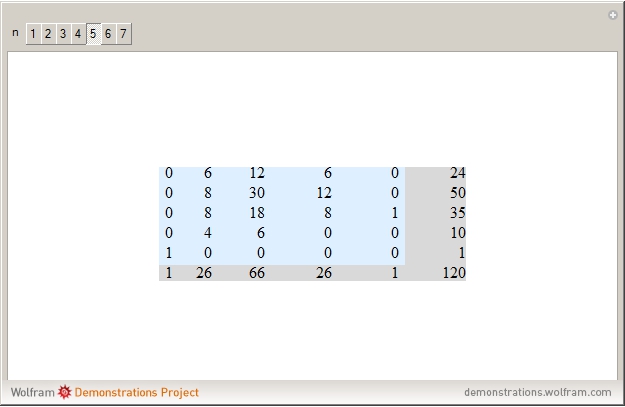
The unsigned Stirling number of the first kind 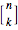 counts the number of permutations of
counts the number of permutations of 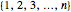 whose cycle decomposition has
whose cycle decomposition has  cycles. For example, the permutation
cycles. For example, the permutation 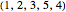 is the mapping
is the mapping 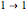 ,
, 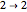 ,
, 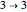 ,
, 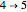 ,
, 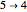 , so its cycle decomposition is
, so its cycle decomposition is  , with four cycles.
, with four cycles.
Contributed by: George Beck (November 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
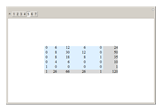
The 1 at position  comes from the identity permutation
comes from the identity permutation 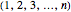 that has
that has  cycles
cycles  row) and one run (column 1).
row) and one run (column 1).
The 1 in the last column comes from the permutation 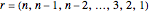 . It has
. It has  runs of length 1. Its cycle decomposition is
runs of length 1. Its cycle decomposition is 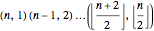 for
for  even and
even and 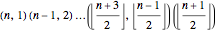 for
for  odd, so
odd, so  has
has  cycles.
cycles.
If a permutation has many cycles, they chain many elements together into longer but fewer runs, which explains the zeros in the lower-right part of the tables.
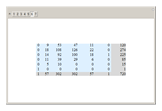
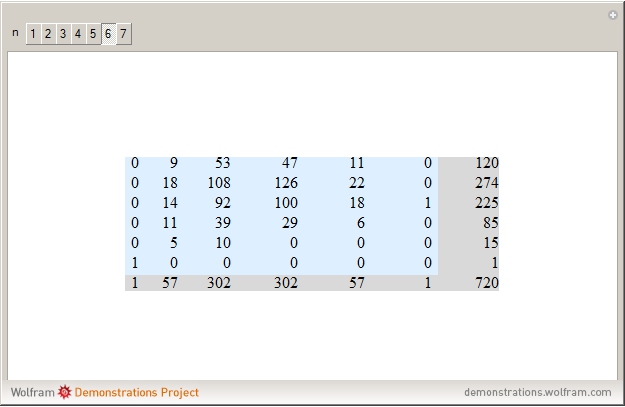
Let us see why the two nonzero entries in the second-to-last row for 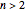 are
are  and
and 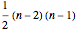 . A permutation with
. A permutation with  cycles consists of one transposition and
cycles consists of one transposition and  singletons (fixed points); there are
singletons (fixed points); there are 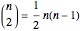 such permutations. If the pair in the transposition are neighbors, there are two runs; there are
such permutations. If the pair in the transposition are neighbors, there are two runs; there are  ways to form a neighboring pair. If the pair are not neighbors, there are three runs and
ways to form a neighboring pair. If the pair are not neighbors, there are three runs and 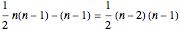 such pairs.
such pairs.
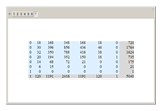
Ignoring the zeros, the first rows of the square tables for 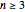 form the following triangle of numbers, which is is symmetric up to
form the following triangle of numbers, which is is symmetric up to 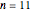 except for two rows. The first terms of the rows of this triangle appear to be the number of binary Lyndon words of length
except for two rows. The first terms of the rows of this triangle appear to be the number of binary Lyndon words of length  A001037 shifted by three and the last terms of the rows appear to be the absolute values of the sequence A038063 shifted by two.
A001037 shifted by three and the last terms of the rows appear to be the absolute values of the sequence A038063 shifted by two.
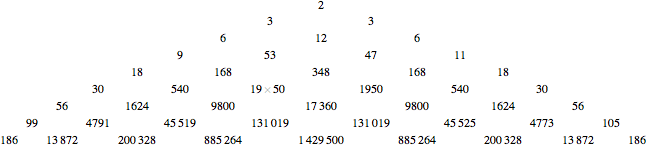
Permanent Citation