Pointwise Properties of Real Functions of a Single Real Variable
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
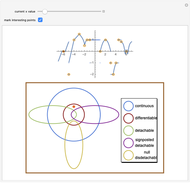
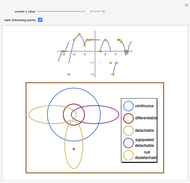
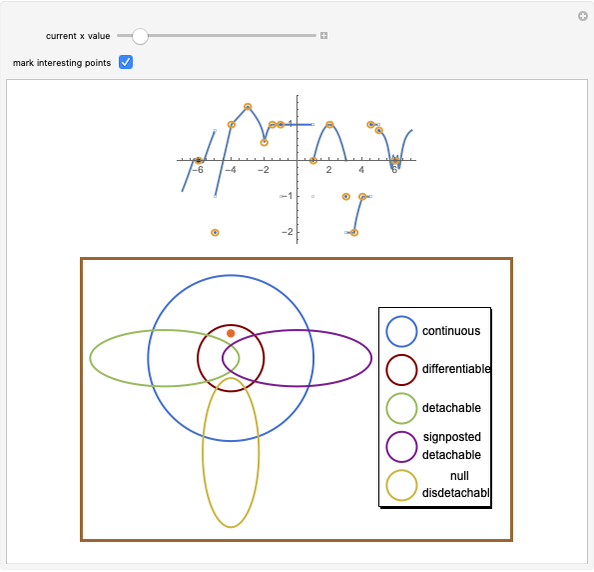
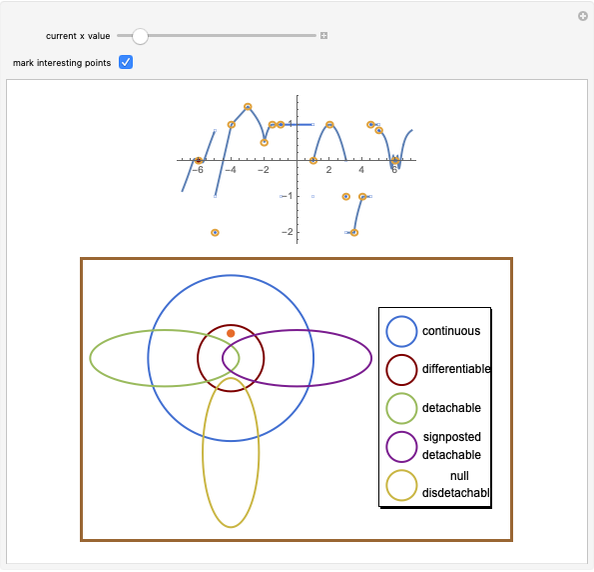
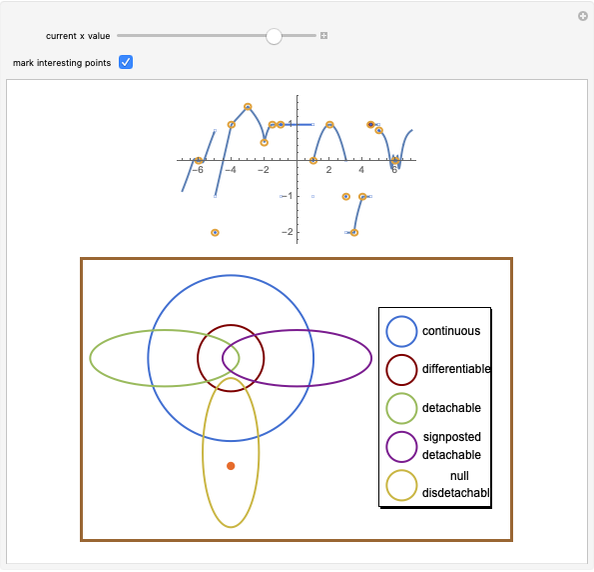
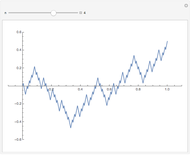
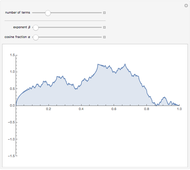
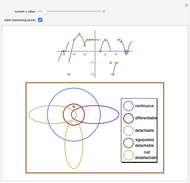
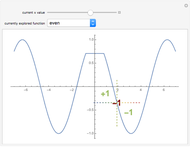
Drag the slider to move through the graph's points. Simultaneously, the function's properties at the visited point are updated in the diagram below using a pink disk. You can check the box "mark interesting points" to highlight some points that demonstrate interesting cases. The graph behaves like Dirichlet's function for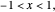 
like the function 
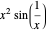at 
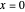and around the point 
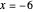, and like the function 
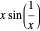at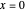 
and around the point 
.
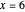Contributed by: Amir Finkelstein (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
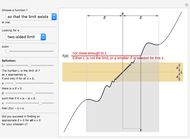
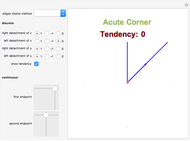
Snapshot 1: the function is differentiable, and not tendable at 
.
Snapshot 2: the function is null disdetachable, and not continuous at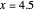 
.
Snapshot 3: the function is detachable, and not continuous at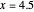 
.
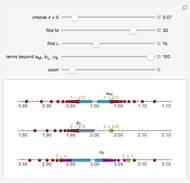
Continuity, differentiability, and tendability are three fundamental properties of single-variable functions. While continuity and differentiability are dependent events (if a function is differentiable then it is continuous), a function may be tendable at a point whether it is differentiable, continuous, or discontinuous there. Tendable functions are classified into three types: detachable, signposted detachable, and null disdetachable, all of which are related to the one-sided limits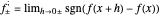 
; a function is said to be detachable if 
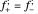, signposted detachable if 
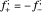, and null disdetachable if 
.
One of the advantages of the detachment operator is that it may be defined also in cases where a function is not differentiable and even not continuous, as shown in this Demonstration.
The terms detachment and tendency are defined in a previous Demonstration. The theory of semidiscrete calculus is given in A. Finkelstein, "The Theory behind the 'Summed Area Table' Algorithm: a Simple Approach to Calculus," arXiv, 2010.
Permanent Citation
Iterating Rational Functions
Philip Lee
Bolzano's Function
Izidor Hafner
Limit of a Function at a Point
Quinn Morris
Bolzano's Continuous but Nowhere Differentiable Function
Izidor Hafner
Riemann's Example of a Continuous but Nowhere Differentiable Function
Michael Trott
Sine Wave Example of the Epsilon-Delta Definition of Limit
Geoffrey F. Miller, Daniel C. Cheshire, Nell H. Wackwitz, Joshua B. Fagan
Epsilon-Delta Definition of Limit
Ferenc Beleznay
Flett's Theorem
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Cesàro Summation
Devendra Kapadia
Limit of the Sum of Two Sequences
Izidor Hafner
-
Slanted Line Integral
Amir Finkelstein -
Extended Discrete Green's Theorem
Amir Finkelstein -
Pointwise Properties of Real Functions of a Single Real Variable
Amir Finkelstein -
Tendency of a Curve
Amir Finkelstein -
A Discrete Green's Theorem
Amir Finkelstein -
A Semi-Discrete Analog to The Mean Value Theorem
Amir Finkelstein -
Double Integrals by Summing Values of a Cumulative Distribution Function
Amir Finkelstein -
Detachment and Tendency of a Single Variable Function
Amir Finkelstein