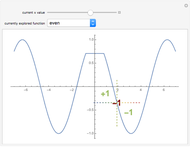
A Semi-Discrete Analog to The Mean Value Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
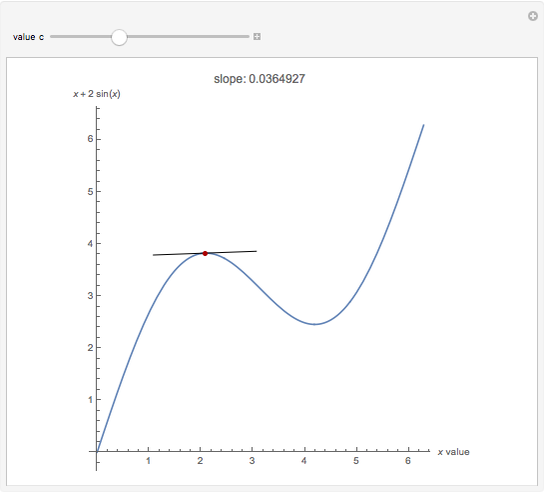
The mean value theorem states that if a function is differentiable in an open interval 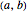 and continuous in its closure
and continuous in its closure 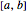 , then there exists a point
, then there exists a point 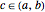 such that
such that 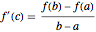 . This theorem's semi-discrete analog suggests that if a function is tendable in
. This theorem's semi-discrete analog suggests that if a function is tendable in 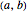 , continuous in
, continuous in 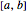 , and also that
, and also that 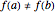 , then for each
, then for each 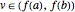 there exists a point
there exists a point 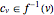 , such that
, such that 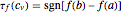 , where
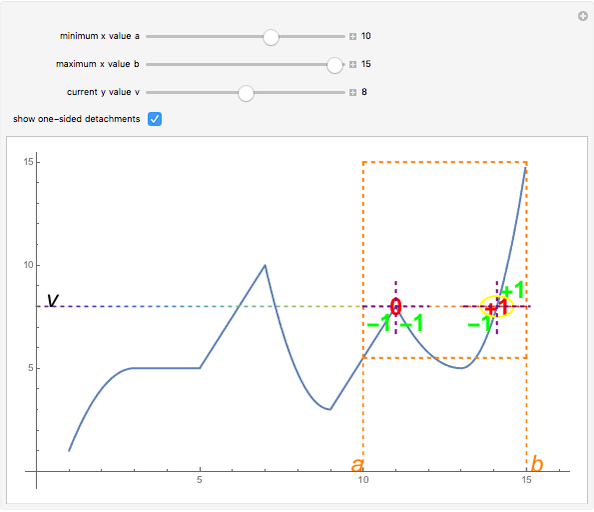
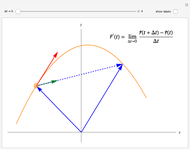
, where 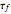 is the function's tendency, and "tendability of a function" means that the tendency operator can be applied to the function. The definition of the tendency operator is given in the Demonstration "Detachment and Tendency of a Single Variable Function". A comparison between the mean value theorem and its semi-discrete analog is found in the details. When compared to the original theorem, this version depicts a trade-off between the functions for which the theorem's correctness holds and the kind of information that the theorem gives. This version is called semi-discrete due to the decisive role of the
is the function's tendency, and "tendability of a function" means that the tendency operator can be applied to the function. The definition of the tendency operator is given in the Demonstration "Detachment and Tendency of a Single Variable Function". A comparison between the mean value theorem and its semi-discrete analog is found in the details. When compared to the original theorem, this version depicts a trade-off between the functions for which the theorem's correctness holds and the kind of information that the theorem gives. This version is called semi-discrete due to the decisive role of the 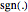 function, whose image is finite. In this Demonstration, you can vary the parameters
function, whose image is finite. In this Demonstration, you can vary the parameters  ,
,  , and
, and  from the theorem's statement to better understand the theorem. The highlighted yellow points
from the theorem's statement to better understand the theorem. The highlighted yellow points  are those whose existence is assured by the theorem.
are those whose existence is assured by the theorem.
Contributed by: Amir Finkelstein (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
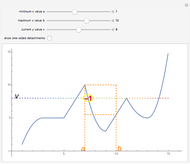
Snapshot 1: setting  ,
, 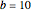 ,
, 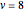 yields only one highlighted point; here the one-sided detachments are omitted
yields only one highlighted point; here the one-sided detachments are omitted
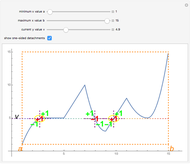
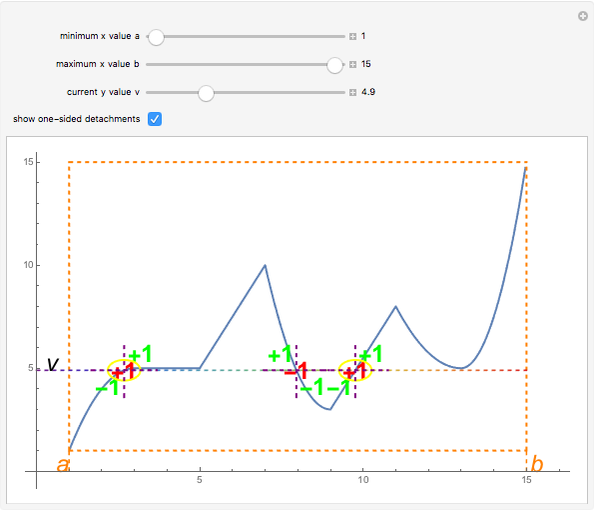
Snapshot 2: setting  ,
,  ,
,  yields two highlighted points; here the one-sided detachments, from which the tendency is calculated, are shown
yields two highlighted points; here the one-sided detachments, from which the tendency is calculated, are shown
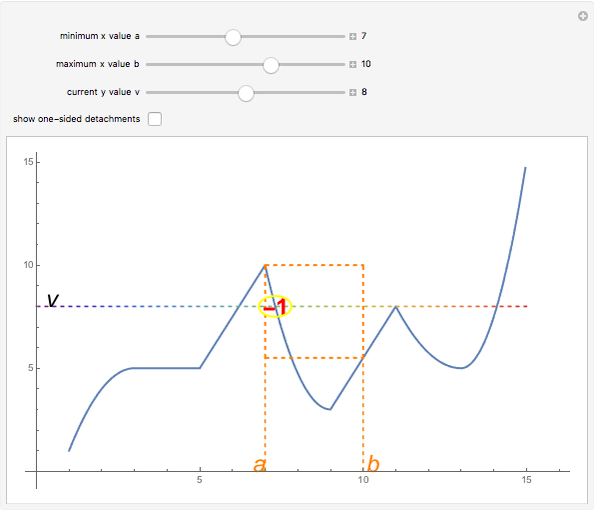
Snapshot 3: setting  ,
,  ,
, 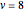 yields one highlighted point; here the one-sided detachments, from which the tendency is calculated, are shown; although there are two points in the chosen interval whose image is
yields one highlighted point; here the one-sided detachments, from which the tendency is calculated, are shown; although there are two points in the chosen interval whose image is  , only one of them is highlighted—the tendency at the other point is zero
, only one of them is highlighted—the tendency at the other point is zero
A short and to the point comparison between the mean value theorem and its semi-discrete analog is depicted in this link.
Permanent Citation