Problems on Circles X: Tangent Circles Generate Ellipses

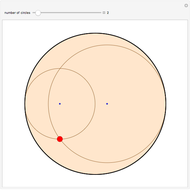
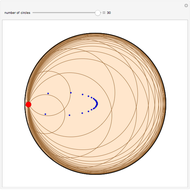
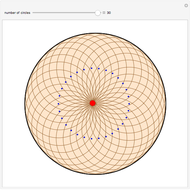
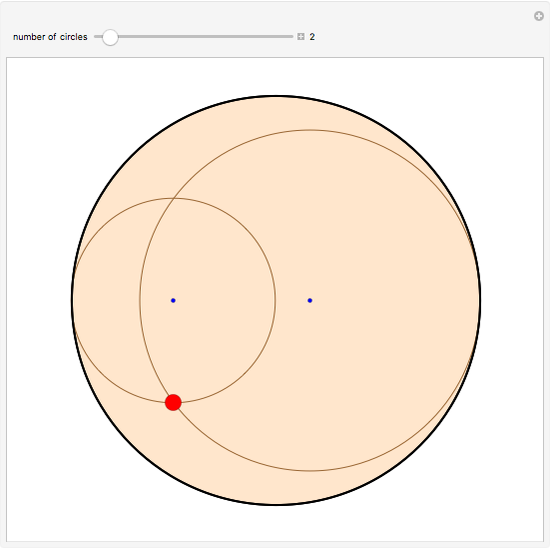
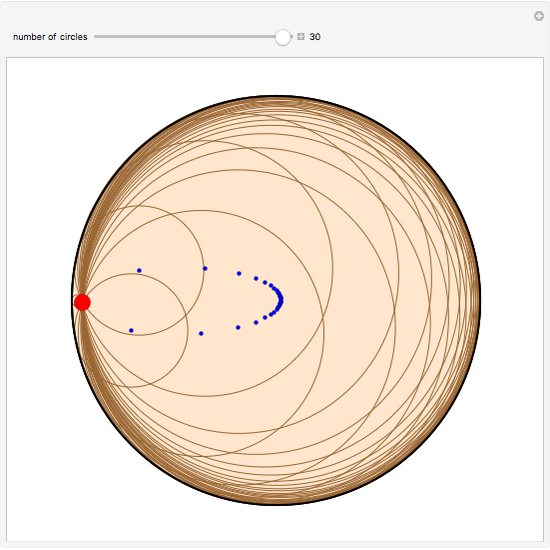
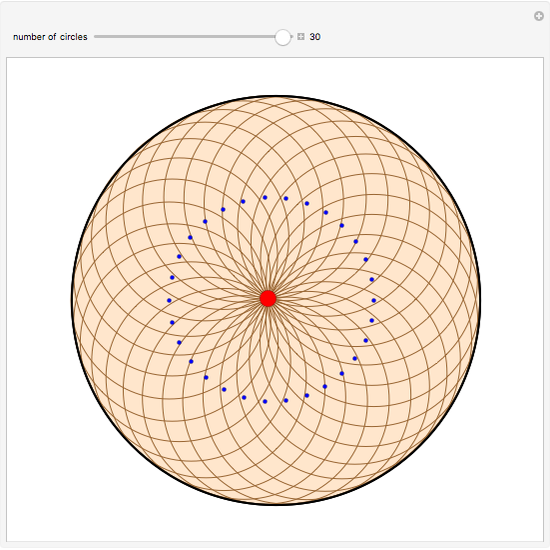
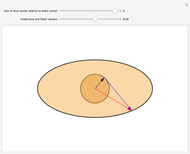
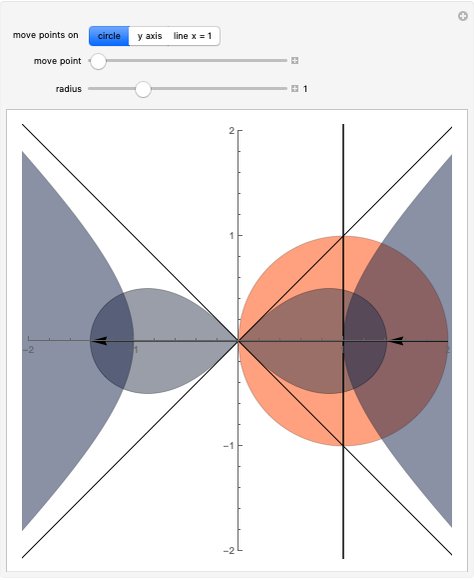
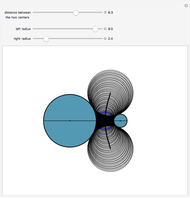
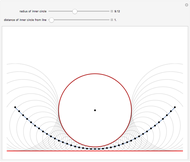
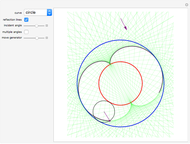
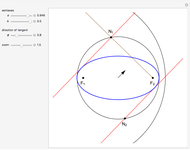
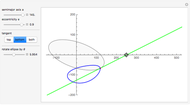
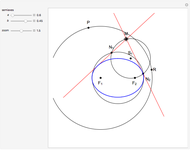
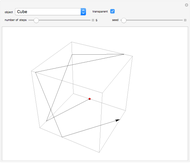
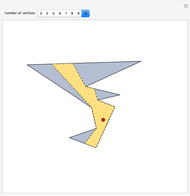
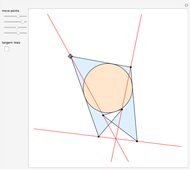
The locus of the center (drawn in blue) of a variable circle (in brown) tangent to a fixed (black) circle and passing through a fixed (red) point inside it is an ellipse. This Demonstration lets you change the position of the fixed point or vary the number of tangent circles passing through it. The point is always one of the foci of the ellipse and is the center when the ellipse is a circle. What happens if the point is chosen outside the circle? Just take out the If line to find out!