Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

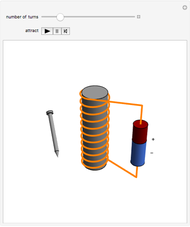
Proton Moving along the Axis of a Charged Ring

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

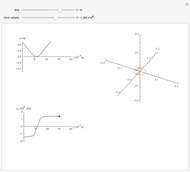
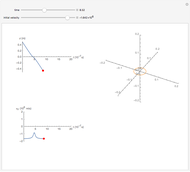
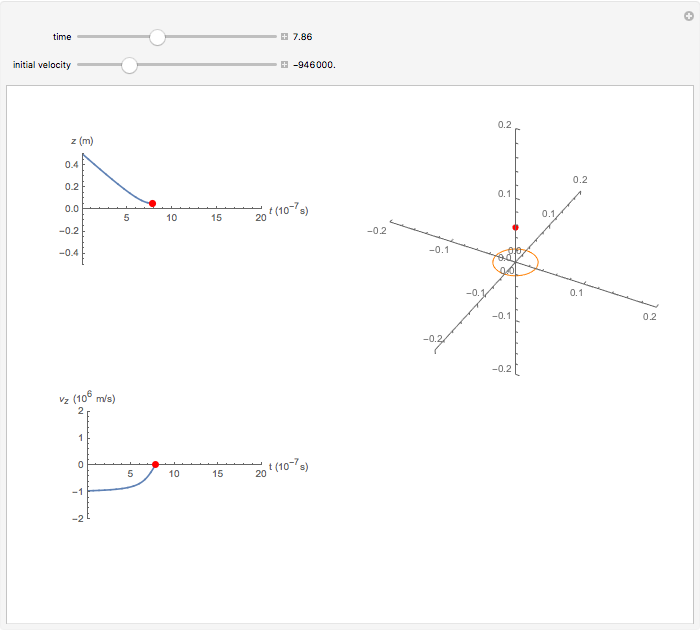
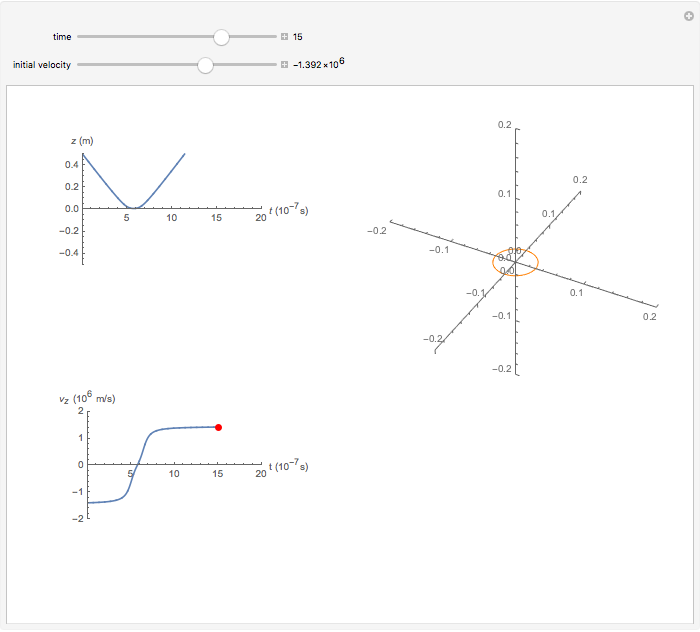
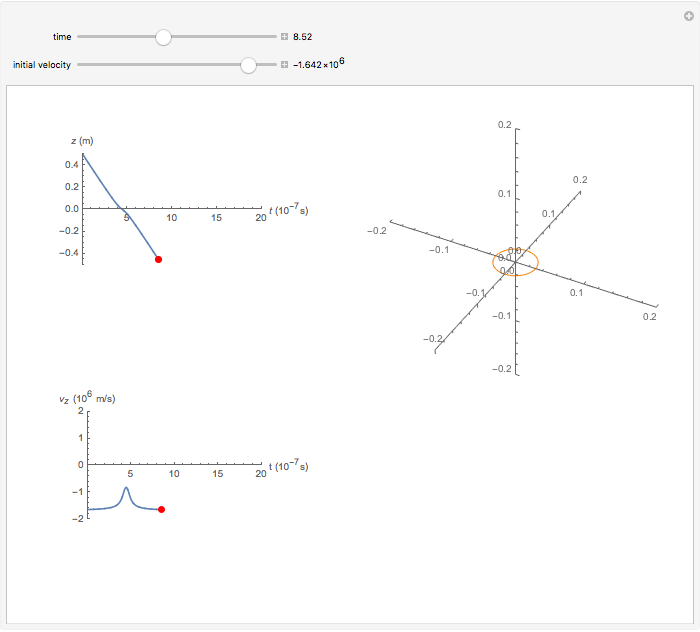
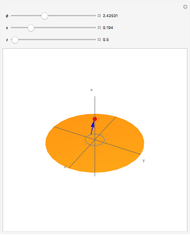
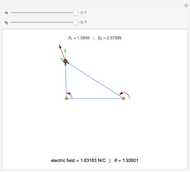
A proton moves along the axis of a uniformly positively charged ring (right figure). If the velocity is small, the ring repels the proton and it bounces backwards, but when the initial velocity is large enough, the proton passes through the ring, reaching a minimum velocity. The position and velocity 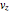are plotted as a function of time on the left. This problem illustrates an example of a force which varies with time.

Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The electric field of the uniformly charged ring at the position on its axis is given by

,

where 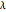is the linear density of charge, taken to be , and 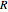is the radius of the ring, equal to 3 cm.

Knowing the initial position and velocity, the electric field is computed and we suppose that the acceleration is constant for a sufficiently small interval of time (here of the order 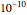s). Then we find the change in position and velocity at the end of the interval, and a new electric field and the acceleration are computed; the procedure is repeated 3000 times.

For further details, see D. Halliday, R. Resnick, and K. S. Krane, Physics, Vol. 2, 5th ed., New York: Wiley, 2006.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send