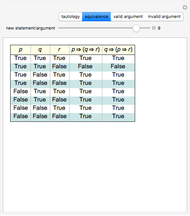
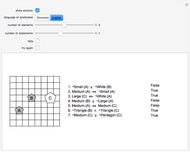
Protothetic

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
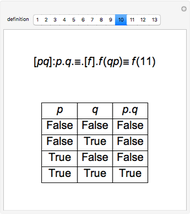
Leśniewski's protothetic is an extended propositional calculus in which all Boolean functions can be defined. The theory also includes a universal quantifier. In 1922, Alfred Tarski established that by employing functional variables and quantifiers, all the functions of propositional calculus can be defined using equivalence as the sole primitive function.
Contributed by: Izidor Hafner (March 2016)
Open content licensed under CC BY-NC-SA
Details
Tarski proved:
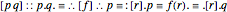 ,
,
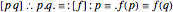 ,
,
each of which can be used in the protothetic as the definition of the conjunction "." by means of the equivalence "≡". Note the use of dots instead of parentheses. Without this usage, the second definition would be:
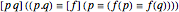 .
.
Here the expression 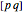 is the universal quantifier. The definitions of True and False can be
is the universal quantifier. The definitions of True and False can be 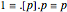 and
and 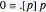 .
.
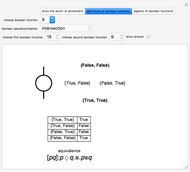
Sobociński discovered that conjunction can be defined by means of equivalence, the universal quantifier, and a variable propositional functor of two arguments.
The first of Sobociński's definitions of conjunction is
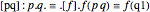 .
.
In more modern notation, the definition could be
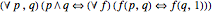 .
.
So 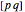 means the universal quantifier for all
means the universal quantifier for all 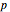 and all
and all  . The range of propositional variables is the set
. The range of propositional variables is the set 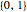 or
or  . The expression
. The expression 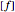 means for all
means for all 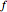 , where the range is the set of all 16 Boolean functions of two arguments. Note also that variables in Sobociński's definitions are not separated by commas.
, where the range is the set of all 16 Boolean functions of two arguments. Note also that variables in Sobociński's definitions are not separated by commas.
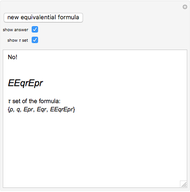
This Demonstration shows all 12 of Sobociński's definitions and an expression that is not a definition of conjunction.
References
[1] B. Sobociński, "An Investigation of Protothetic," Polish Logic 1920-1939 (S. McCall, ed.), Oxford: Oxford University Press, 1967 pp. 201–206.
[2] J. T. J. Srzdnicki and Z. Stachniak, eds., S. Leśniewski's Lecture Notes in Logic, Dordrecht: Kluwer Academic Publishers, 1988 pp. 2–28.
Snapshots
Permanent Citation