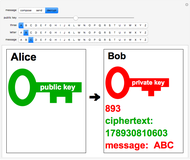
The RSA algorithm for public-key encryption was originated by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT in 1977. Several similar methods had been proposed by earlier workers. The algorithm is based on the fact that it is far more difficult to factor a product of two primes than it is to multiply the two primes. Even the most powerful modern supercomputers would require more time than the age of the universe to factor a 400-digit number. (This might change if quantum computers ever become operational.)
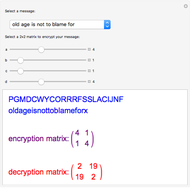
In this Demonstration, the RSA algorithm is simulated using much smaller randomly chosen prime numbers,  and
and  both less than 100. The public key, which is made freely available to Alice and all other users, consists of the two numbers
both less than 100. The public key, which is made freely available to Alice and all other users, consists of the two numbers  and an exponent
and an exponent  , which is an odd integer relatively prime to
, which is an odd integer relatively prime to  between 1 and
between 1 and  . (Here
. (Here  is Euler's totient function, the number of positive integers less than
is Euler's totient function, the number of positive integers less than  and relatively prime to
and relatively prime to  .) For simplicity, take
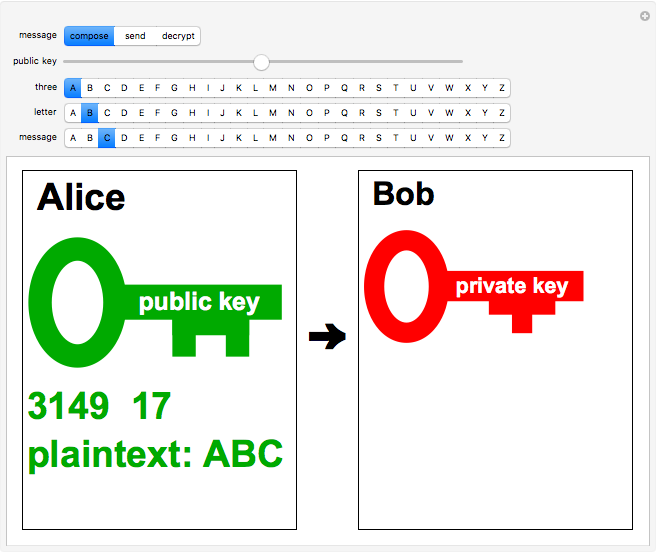
.) For simplicity, take  and also limit messages to three letters, such as XYZ. This constitutes the plaintext and is converted into an integer
and also limit messages to three letters, such as XYZ. This constitutes the plaintext and is converted into an integer  using, for example, ASCII codes. The corresponding ciphertext
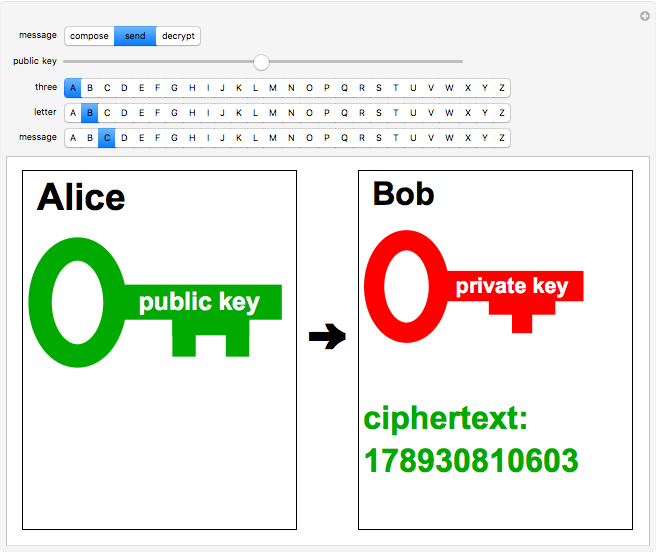
using, for example, ASCII codes. The corresponding ciphertext  is computed using
is computed using  .
.
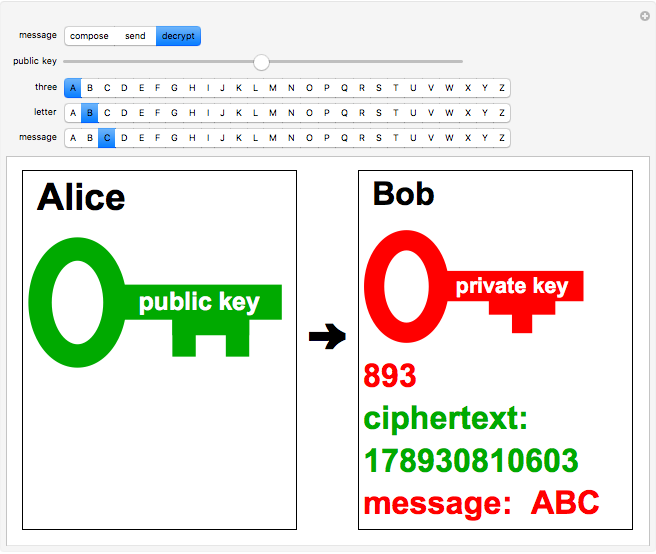
Only the recipient Bob has access to the private key, which is an integer exponent  , a modular inverse to
, a modular inverse to  such that
such that 
 . To determine
. To determine  , a codebreaker would need to find the prime factors of
, a codebreaker would need to find the prime factors of  , which, as noted earlier, is hopefully impossible. The plaintext is recovered using
, which, as noted earlier, is hopefully impossible. The plaintext is recovered using  . The method works since
. The method works since  (mod
(mod  ), with application of Fermat's little theorem. The public and private keys can periodically be changed according to some prearranged schedule.
), with application of Fermat's little theorem. The public and private keys can periodically be changed according to some prearranged schedule.
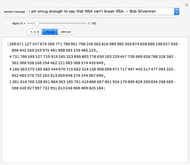
By inputting the public key  and the three-part ciphertext
and the three-part ciphertext  , Bob can recover the plaintext message.
, Bob can recover the plaintext message.
[less]