Radial Velocity Curve Fitting

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
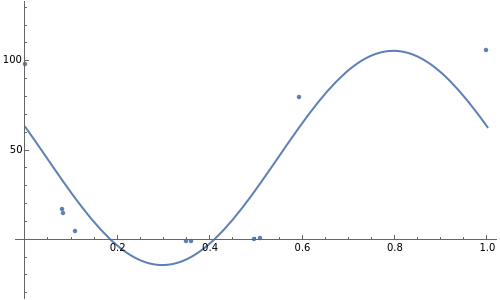
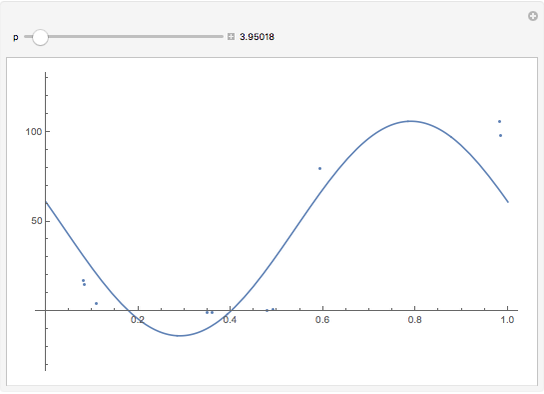
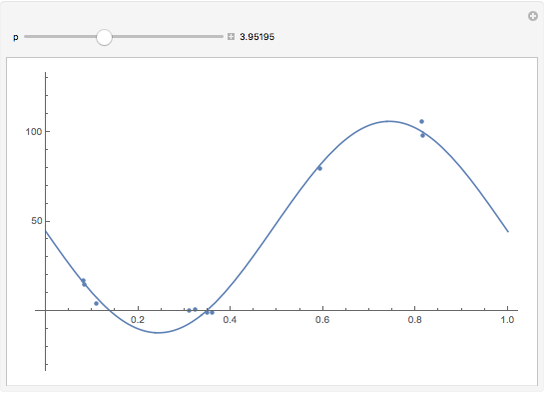
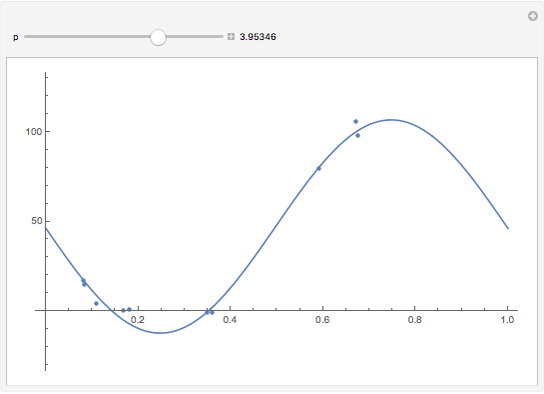
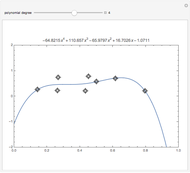
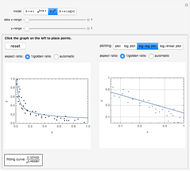
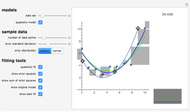
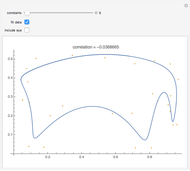
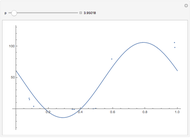
This Demonstration shows 10 radial velocity data points folded over a varying period. A sinusoidal fit is calculated using a nonlinear regression technique. This is supposed to show the difficulty of finding a single value for a period based on such a small number of data points. The data comes from real observations made by UCL Astronomy students in 2006 and 2010 using a 1.52 m telescope at OHP, France.
Contributed by: Jakub Bochinski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Nonlinear curve fitting is based on a mathematical concept of regression analysis, which tries to minimize differences between the fit and nearby data points (residuals). This can be done for any given type of function and a possibly unlimited number of variables. Mathematica can compute nonlinear regression to fit a model sinusoidal function
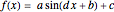
to a dataset, taking into account uncertainties associated with each data point separately. In the equation, 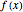 is a radial velocity,
is a radial velocity,  is a Julian date (or phase), and
is a Julian date (or phase), and  ,
,  ,
,  ,
,  are adjustable parameters. It is clear that this function can be stretched and shifted along either axis, but not tilted sideways.
are adjustable parameters. It is clear that this function can be stretched and shifted along either axis, but not tilted sideways.
Permanent Citation