Fitting an Ellipse to the Orbit of a Star near the Galactic Center

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
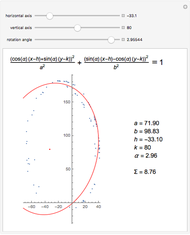
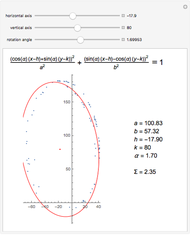
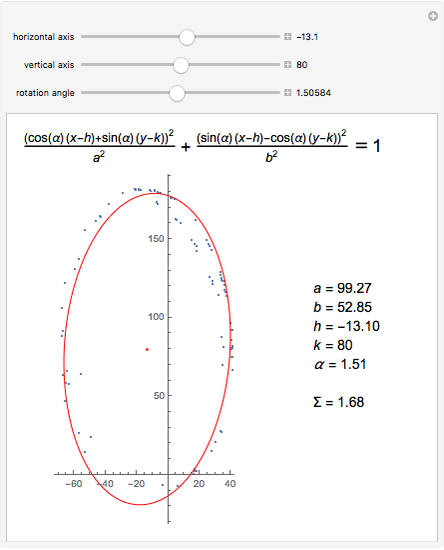
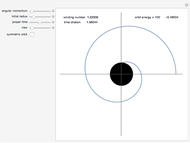
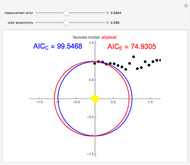
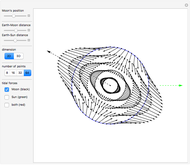
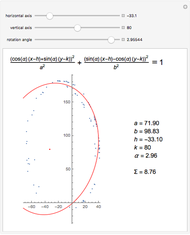
This Demonstration shows how the equation for the best-fitting ellipse can be determined for several predefined points in the Cartesian plane. The points are the locations of a star known as S2 near the center of our galaxy.
[more]
Contributed by: Weronika Lachtara and Jakub Bochinski (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The data points used in this Demonstration are the coordinates representing the position of star S2 orbiting around Sagittarius A*. They have been collected by the Very Large Telescope, Keck, and NTT since 1992.
Sagittarius A* is the strong radio source considered to be the center of our Milky Way galaxy and where a supermassive black hole might be situated. Since star S2 is drifting around an elliptic path, according to Kepler’s laws of planetary motion, the mass of an object at the foci of the ellipse can be determined.
Reference
[1] S. Gillessen, F. Eisenhauer, T. K. Fritz, H. Bartko, K. Dodds-Eden, O. Pfuhl, T. Ott, and R. Genzel, "The Orbit of the Star S2 around Sgr A* from VLT and Keck Data," The Astrophysical Journal, 707, 2009 pp. L114–L117.
Permanent Citation