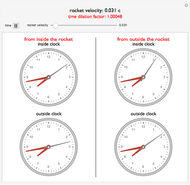
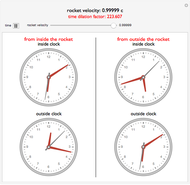
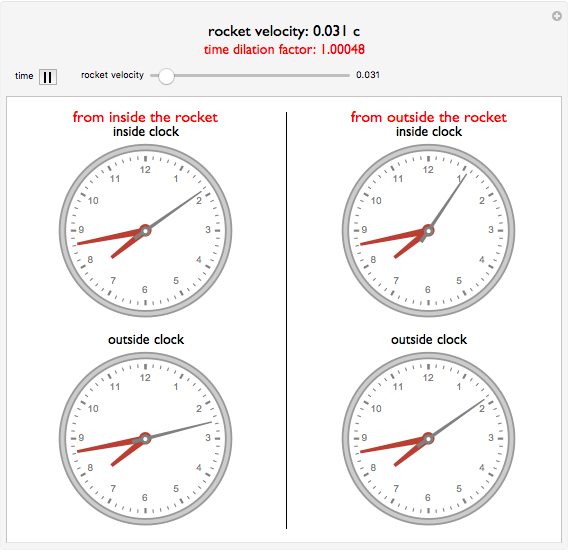
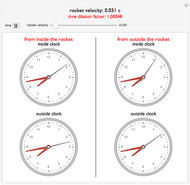
This Demonstration shows an example of relativistic time dilation as described by the Lorentz transformation. When the velocity of a rocket ship is zero, all clocks display the same time. The faster the rocket's velocity, as represented by the slider, the greater the time dilation factor becomes. This means that the stationary observer, assumed to be in an inertial frame, perceives the rocket's clock as moving more slowly. You can then see the resulting discrepancies in time measurement from both the perspectives of a traveler inside the moving rocket ship and that of a stationary observer. Gravitational effects on time dilation are not considered.