Robustness of Student t in the One-Sample Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
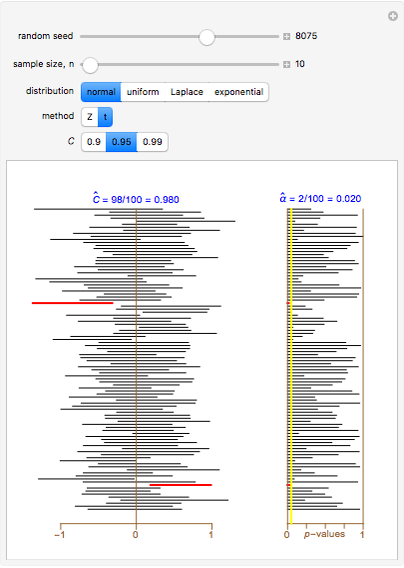
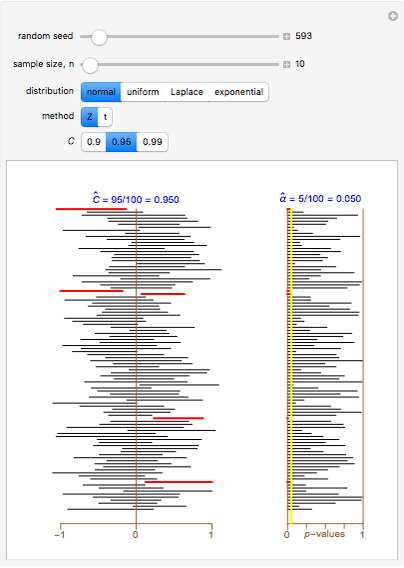
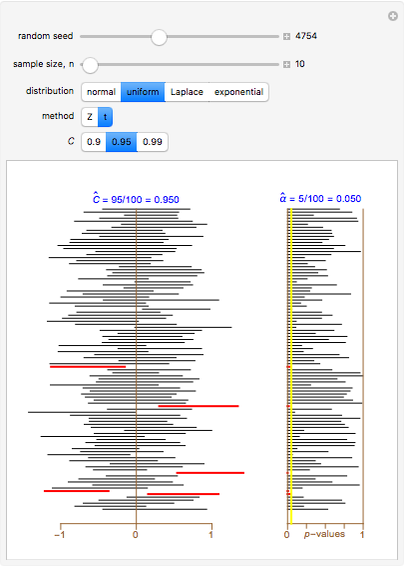
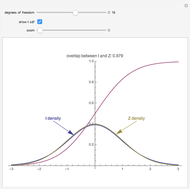
Level  confidence intervals and
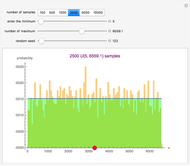
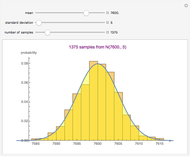
confidence intervals and  -values are shown for 100 simple random samples of size
-values are shown for 100 simple random samples of size  drawn from the specified population with mean
drawn from the specified population with mean  and standard deviation
and standard deviation  . The
. The 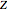 and
and  methods are compared for calculating the confidence intervals and
methods are compared for calculating the confidence intervals and  -values. The
-values. The 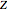 method is based on the normal distribution using the estimated standard deviation in place of the unknown
method is based on the normal distribution using the estimated standard deviation in place of the unknown  . The
. The 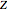 method is approximately valid for
method is approximately valid for  large enough for all distributions considered in this Demonstration. The
large enough for all distributions considered in this Demonstration. The  method uses the Student
method uses the Student  -distribution with
-distribution with  degrees of freedom; it is exact in the case of the normal distribution and is approximate for the other distributions considered in this Demonstration.
degrees of freedom; it is exact in the case of the normal distribution and is approximate for the other distributions considered in this Demonstration.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
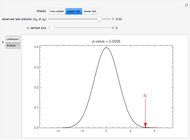
Each of the distributions used has population mean 0 and variance 1, as indicated on the scale at the bottom of the left panel. The  -value is for testing
-value is for testing  versus
versus  . Of the three non-normal distributions considered, the
. Of the three non-normal distributions considered, the  methods work almost as well for the uniform and Laplace distributions as the normal for sample sizes as small as 10, but for such small samples the exponential distribution generates
methods work almost as well for the uniform and Laplace distributions as the normal for sample sizes as small as 10, but for such small samples the exponential distribution generates  intervals and
intervals and  -tests that are not conservative. As
-tests that are not conservative. As  increases, there is an improvement.
increases, there is an improvement.
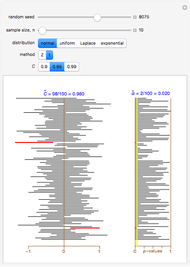
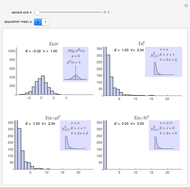
Snapshot 1: setting 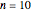 and using the
and using the  -test method with the normal distribution and
-test method with the normal distribution and  , we find after some simulations that the empirical values for the estimates
, we find after some simulations that the empirical values for the estimates  and
and  are close to their theoretical values of 0.95 and 0.05
are close to their theoretical values of 0.95 and 0.05
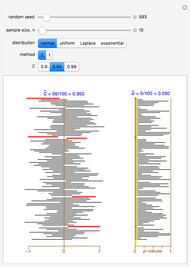
Snapshot 2: as in Snapshot 1, but using the 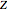 -test instead of the
-test instead of the  -test; after a large number of simulations, we see the empirical coverage probability is about 92%, which means the confidence intervals are too narrow; similarly the type I error at 8% is well above its nominal 5% value; this demonstrates that the
-test; after a large number of simulations, we see the empirical coverage probability is about 92%, which means the confidence intervals are too narrow; similarly the type I error at 8% is well above its nominal 5% value; this demonstrates that the 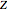 -test method is not conservative in small samples
-test method is not conservative in small samples
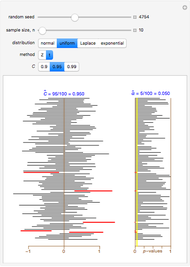
Snapshot 3: as in Snapshot 1, but with the uniform distribution; no observable difference from the normal population case
Snapshot 4: as in Snapshot 1, but with the Laplace distribution; this distribution has thicker tails than the normal, but even here the empirical coverage is not significantly different from the nominal 95% level, illustrating the robustness of the  -distribution method
-distribution method
Snapshot 5: as in Snapshot 1, but with the exponential distribution; this distribution is right-skewed and very non-normal and in this case the  method yields an empirical coverage rate of about
method yields an empirical coverage rate of about 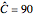 % instead of the nominal 95% value; the
% instead of the nominal 95% value; the  method is not even conservative in this case
method is not even conservative in this case
Snapshot 6: as in Snapshot 5, but the sample size is increased to  ; the
; the  methods have improved and only slightly overstate the statistical significance of the test
methods have improved and only slightly overstate the statistical significance of the test
Snapshot 7: as in Snapshot 6, but the sample size is increased to  ; now the approximation is accurate
; now the approximation is accurate
Permanent Citation