Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Six Incircles in an Equilateral Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

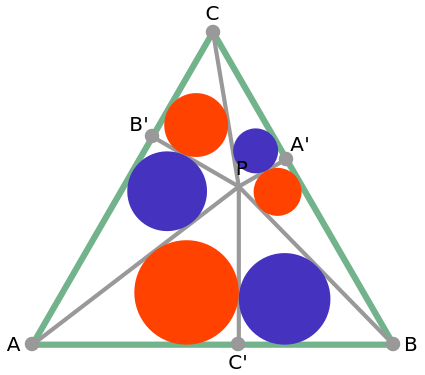
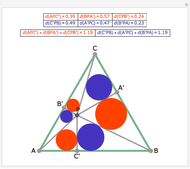
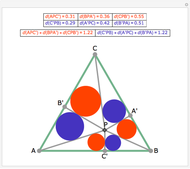
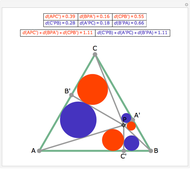
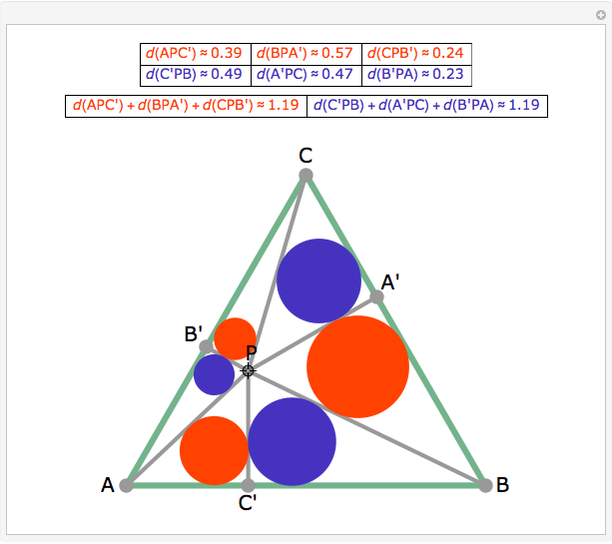
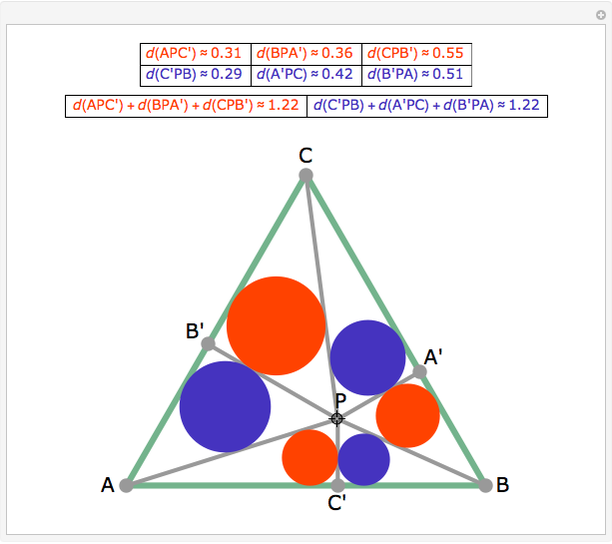
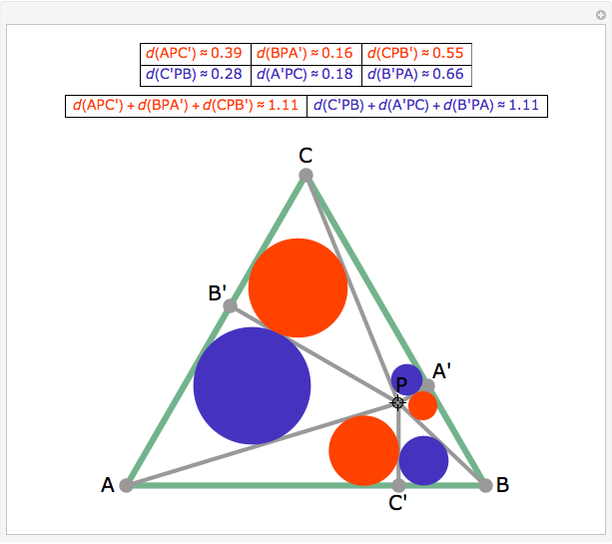
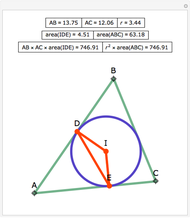
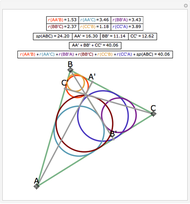
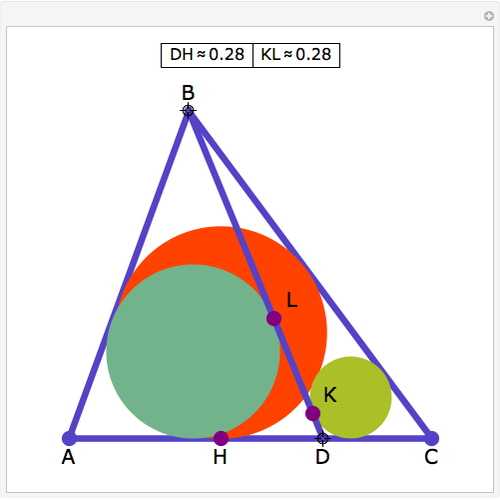
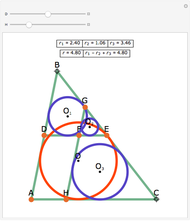
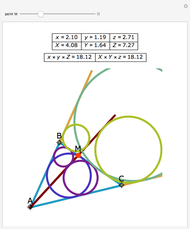
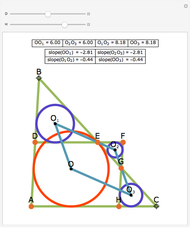
From an interior point P of an equilateral triangle ABC draw lines perpendicular to the sides. Let A', B', and C' be the points on the sides opposite A, B and C. Inscribe circles in the six subtriangles. Let (XYZ) denote the diameter of the incircle in triangle XYZ.

[more]

Then the sum of the diameters of the red circles equals the sum of the diameters of the blue circles:

(APC') + (BPA') + (CPB') = (C' PB) + (A' PC) + (B' PA)

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information see Six Incircles in an Equilateral Triangle.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send