Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Solid-Solid-Liquid Equilibrium

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

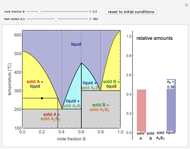
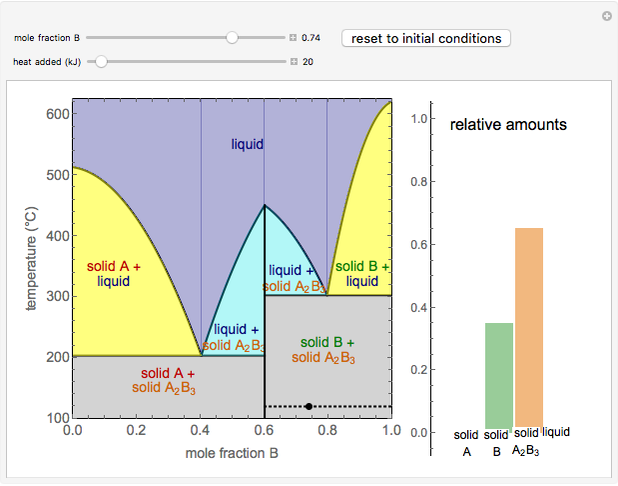
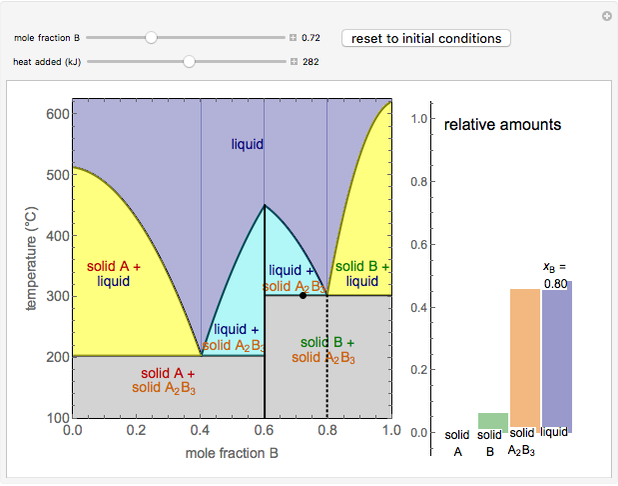
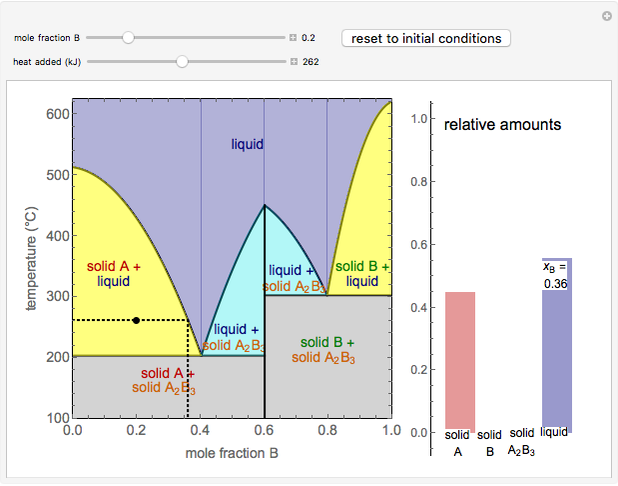
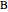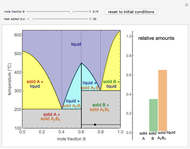
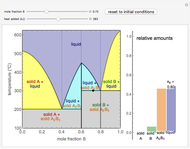
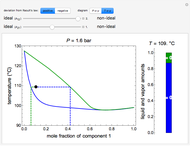
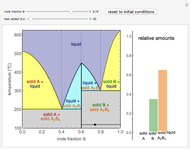
This Demonstration illustrates the behavior of a system of two pure substances ( and ) and a solid compound of the two (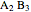). Solid-liquid equilibrium and solid-solid-liquid equilibrium are both represented in the phase diagram. Mixtures of pure solids are immiscible. 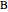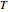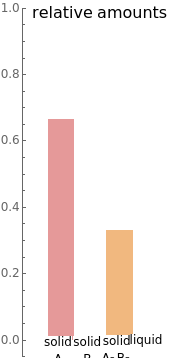The relative amounts of the four possible phases, given the temperature and mole fraction of (represented by the black point in the -- diagram), are shown in the bar graph to the right of the diagram. The mole fraction of 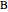in the liquid phase (mixture of liquid 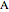and liquid 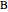) is given above the liquid bar in the bar graph. Since each solid phase is pure for the respective solid component, their mole fractions are omitted.

[more]

You can move the black point by adjusting the mole fraction slider and the heat-added slider. When heat is added, the temperature will increase, except when the point is on one of the two horizontal lines, located at about 200 °C and 300 °C. On these lines, three phases can exist in equilibrium: solid and liquid, in addition to either solid or solid . A mole balance can be used to find the relative amounts of each phase on these lines. Before the temperature can increase or decrease, one phase must melt or one phase must freeze, respectively. The amount of heat added is meant to illustrate what phases can be present in this system, and how a given temperature and mole fraction of can result in multiple different phase distributions; it is not meant to represent an actual value for a real system. In the two phase regions, the relative amounts of each phase are given by the lever rule, and the mole fraction of in the liquid phase is shown by a vertical dashed line.

[less]

Contributed by: Megan E. Maguire (November 2014)
Additional contributions by: Rachael L. Baumann
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The lever rule is used to find the relative molar contents of each phase. An example in the solid 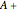liquid region is given by:

,

,

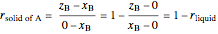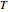where is the overall mole fraction of the mixture (the mole fraction of the point in the -- diagram), 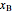is the mole fraction of 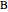in the liquid phase, the mole fraction of 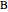in the solid 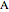phase is zero, 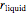is the relative amount of liquid, and 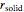is the relative amount of solid .

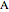When the system is in solid-solid-liquid equilibrium, the relative amounts of each phase are found from mass balances. For example, using a value of 10.0% melted and an initial mole fraction of 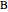of 0.700 in the diagram:

1. Determine the initial mole fraction of :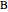

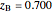
2. Determine the mole fraction of component 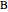in each phase:

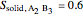
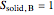
3. Set a basis for the amount of total moles in the system:

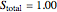
4. Determine the percentage melted:

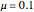
5. Determine the amount of liquid in the system:

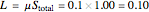
6. Perform a mole balance on the whole system:

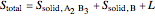
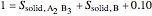
7. Perform a mole balance on component :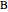

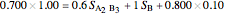
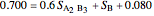
8. Simultaneously solve the equations 6 and 7 with the unknown variables (the number of equations should equal the number of unknown variables):

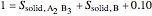
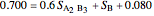
9. Relative amounts of each phase:

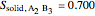(relative amount of solid )

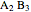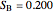(relative amount of solid )

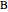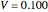(relative amount of liquid)

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send