Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Spherical Law of Cosines

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

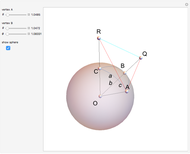
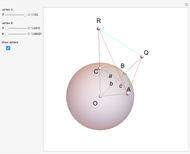
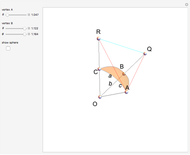
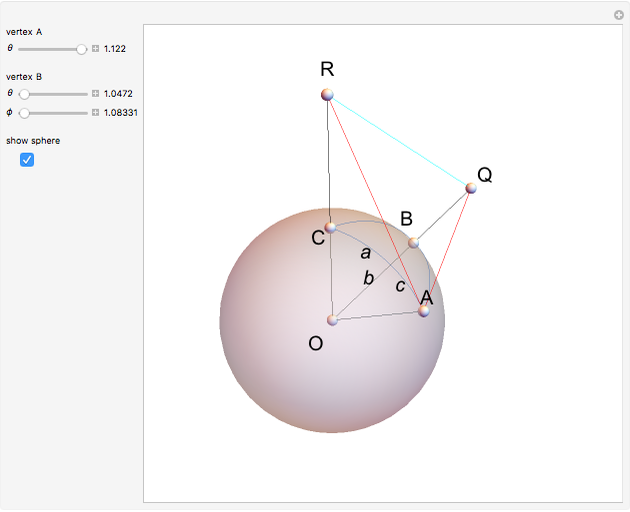
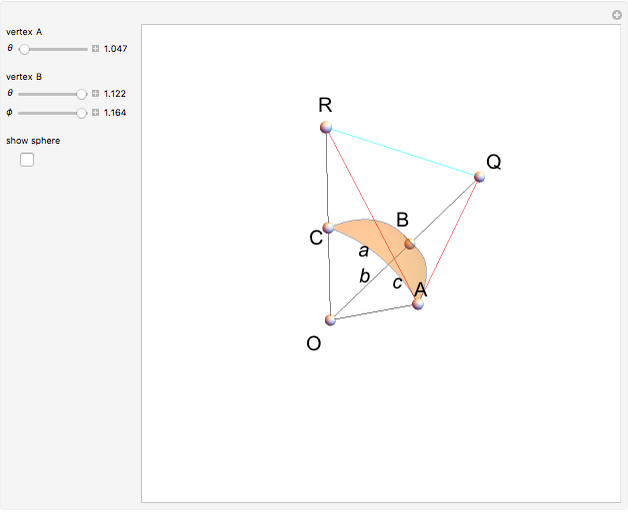
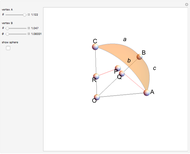
Draw a spherical triangle on the surface of the unit sphere with center at the origin . Let the sides (arcs) opposite the vertices have lengths , and , and let be the angle at vertex . The spherical law of cosines is then given by , with two analogs obtained by permutations.

Contributed by: Izidor Hafner (February 2017)
Open content licensed under CC BY-NC-SA

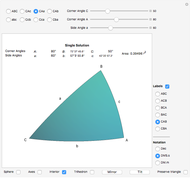
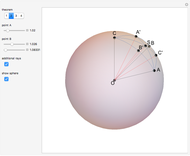
Snapshots

Details

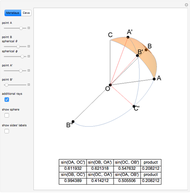
Let be the plane tangent to the sphere at , and let and . Then , , and . Express the length of in two ways using the usual planar law of cosines for the triangle in the plane :

.

With the triangle , the law of cosines gives

.

The two equalities give

.

Reference

[1] Wikipedia. "Spherical Law of Cosines." (Feb 22, 2017) en.wikipedia.org/wiki/Spherical_law_of _cosines.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send