Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Spinning Mass with Variable Radius

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

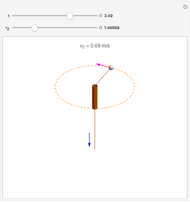
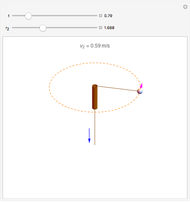
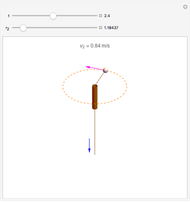
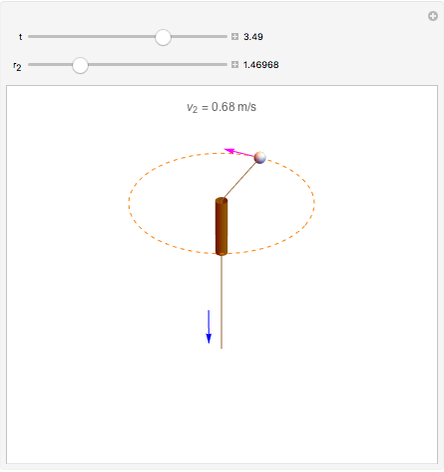
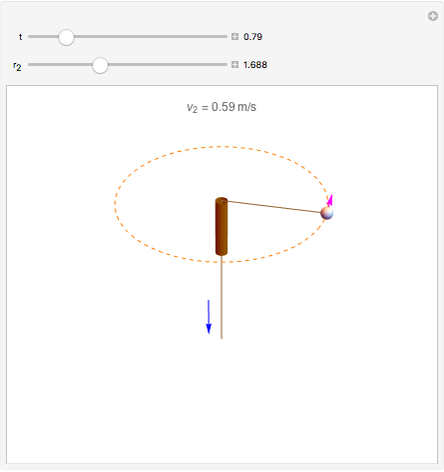
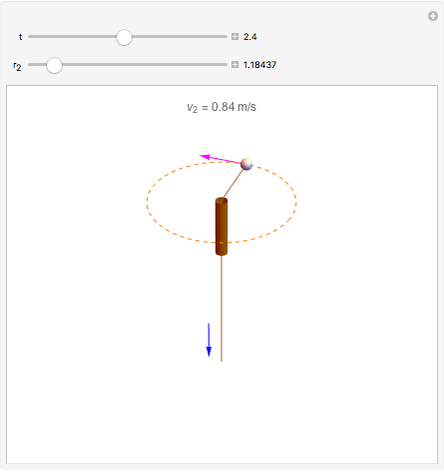
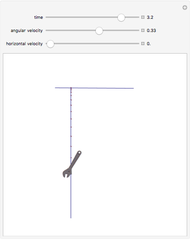
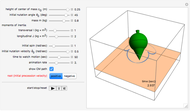
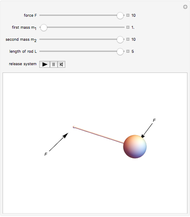
A small ball is attached to a string passing through a pipe as shown in the figure. The ball is initially spinning around in a circle of radius 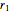with tangential velocity (the instantaneous linear velocity at some point). When the string is pulled down, the velocity of the ball increases as a consequence of the conservation of angular momentum.

Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

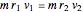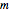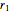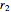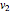We can write the conservation of angular momentum as , where is the mass, and are the initial and final radii, and and are the initial and final tangential velocities; then 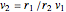. For simplicity, 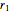and are chosen equal to 1.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send