Details

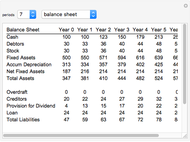
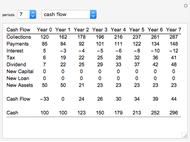
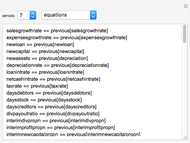
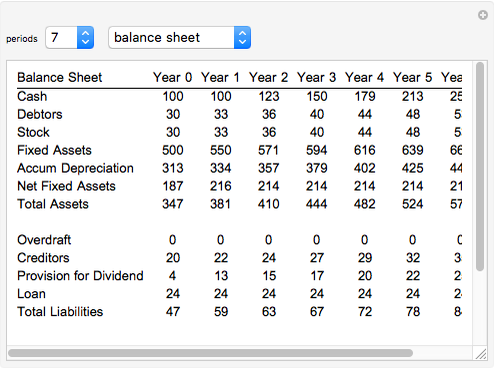
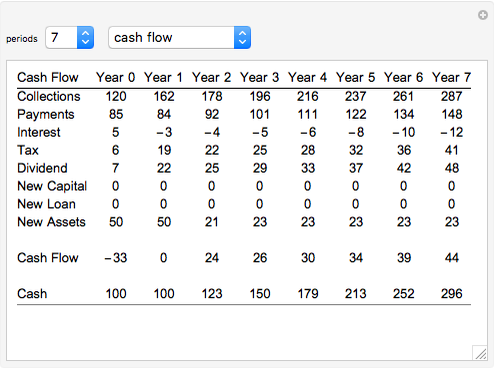
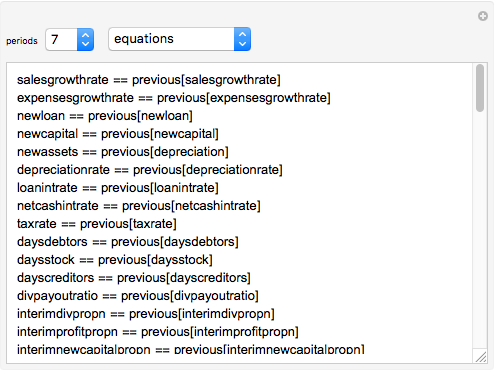
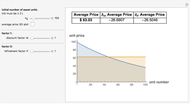
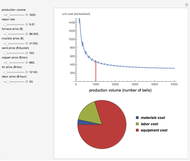
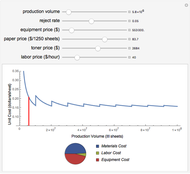
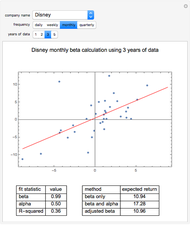
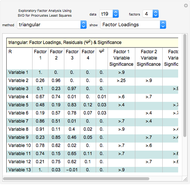
The technique being demonstrated is one of efficiently solving generic systems of equations in large-scale economic models, in this case a corporate financial model. Essentially, this Demonstration provides equation-based spreadsheet functionality in Mathematica that can be used as an exo-equation framework, either directly or for optimization.

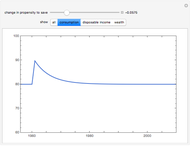
Implicit in this method is the ability to specify various levels of dependency in the equations. In the financial model example provided, all the initial inputs are well understood and so the model is fully specified from the outset. For example, in this example model, the sales growth each year is taken to be the same as the previous year. Of course this is a very simple assumption and in most practical projects this will not be the case. Generally sales growth will derive from a competitive market share model in terms of units and price.

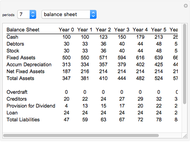
The corporate model provided as an example could be used to optimize any intermediate or final variable such as minimizing investment, maximizing the net present value (NPV) of residual income (and thus goodwill value). For example, it may be used for a corporate projection of 500 months of a toll road operation. While spreadsheets released in the last few years are able to achieve this in terms of column dimension, a corporate model of this magnitude is extremely difficult if not impossible to manage.

This Demonstration also illustrates how the circularity of interest is dealt with in profession corporate models. In order to retain emphasis on the generic solution of equations, which is the purpose of this Demonstration, it has been left to the user to add blocks of equations and assumptions for competitive market share models as input and discounted free cash flow valuation models as additional output. A backward propagation function ("next") may be readily implemented for this purpose in the same way as the forward propagation function ("previous") provided.

The heritage of the generic spreadsheet-like functionality in this Demonstration is to be found in Dinic's method [1], a seminal contribution to calculating maximum flow in networks. The method has been applied to topological sequencing of undirected equations in the absence of dependency ([2], [3], [4]). In Dinic's method, a network is constructed with directed edges from a source to each node representing an equation, from each node to the variables comprising the node equation, and finally from each variable to a sink. The sequenced network of equations is then determined by topologically sorting the network after reversing the direction of the edges carrying positive flows given the maximum flow in the network.

While Dinic's method for determining maximal flow may be substituted by another convenient algorithm such as Edmonds–Karp or Goldberg–Tarjan, the need to determine maximum flow and indeed to prepare the extensive set of edges from the source and to the sink may be obviated entirely by modern combinatorical techniques. Maximal clique bipartite matching aligns equation nodes to constituent variables, such that the edges in the independent set are never incident to the same node vertex.

However, Dinic's method is still required for the second phase, which is to reverse certain edges, analogous to what Dinic calls blocking flows, in order to form an acyclic directed graph that is amenable to topological sorting. There are two difficulties inherent in this second phase. The first issue is a lack of control over inputs and outputs. Any variable may be arbitrarily regarded as an input to the network, leading to some other variables becoming outputs. The second issue is related: Dinic's solution is indeterminate, in that there are two possible results, one using a topological sort of the prima facie acyclic network and another from the topological sort of the same network with all edges reversed.

These two difficulties of Dinic's method may be overcome by recognizing that each equation node will have a vertex out-degree of one. Additional nodes may be introduced to initiate vertices with out-degree of one, having newly introduced edges to the input variables. Thus an arbitrary orientation of the inputs and outputs is avoided and it is at once found that the reverse solution of the Dinic method is the natural solution that avoids rotational indeterminacy. In most applications there will be minimal additional encumbrance incurred in specifying whatever input variables may eventually be selected. However, specifying input variables remains optional and there may even be some serendipity in allowing the algorithm to perform in various modes in order to recognize new and perhaps more stable patterns of control variables.

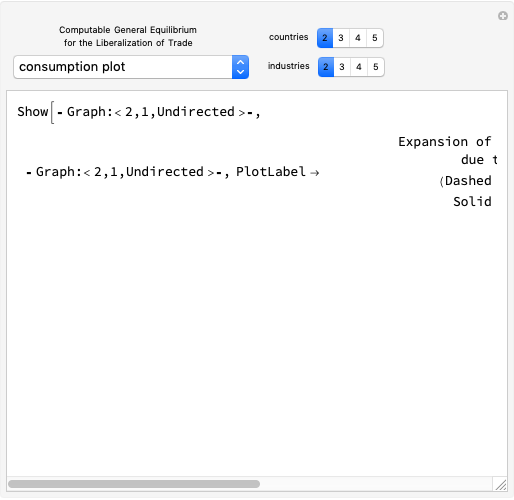
A primary application of the concept in this Demonstration is expected to be in massively extensive nonlinear exo-model networks for use in computable general equilibrium optimization. For example, nonlinear climate computable general equilibrium models (climate CGEs). Such models illustrate two of the major advantages of the algorithm. The first is that the large generic set of equations may be controlled through a small set of input variables so all state variables do not need to be controlled as part of the optimization. This relegates the majority of state variables to merely convenient intermediate points, even when these state variables are employed in constraints. A second advantage is that many complicated equations (with transcendental functions, sign switches, etc.) are solved in short, simple, and very fast steps external to the optimization function. It may be noted that models run in a few seconds depending upon computer speed.

References

[1] E. A. Dinic, "Algorithm for Solution of a Problem of Maximum Flow in a Network with Power Estimation," Soviet Math. Dokl. 11(5), 1970. http://www.cs.bgu.ac.il/~dinitz/D70.pdf.

[2] A. M. Indrani, "Some Issues Concerning Computer Algebra," in AToM (Appendix A), Montreal, Quebec Canada: Modelling, Simulation and Design Lab, School of Computer Science, McGill University, 2003. http://moncs.cs.mcgill.ca/people/indrani/publications.dtml.

[3] W. Xu, "The Design and Implementation of the Modelica Compiler," M.S. thesis, School of Computer Science, McGill University, 2005. http://msdl.cs.mcgill.ca/people/wxu/doc_file/thesisFinalVersion.pdf.

[4] S. J. Nettleton, "Benchmarking Climate Change Strategies under Constrained Resource Usage," Ph.D. dissertation, Australian Digital Theses Program, University of Technology, Sydney, 2010. http://utsescholarship.lib.uts.edu.au/iresearch/scholarly-works/handle/2100/1012.