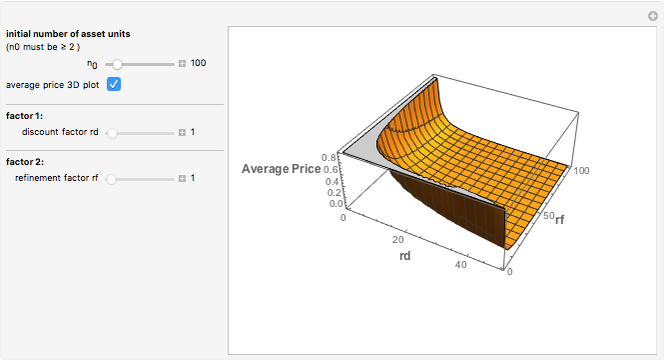
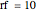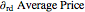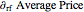The variable 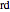 is the discount rate of the next unit bought compared to the price of the preceding unit.
is the discount rate of the next unit bought compared to the price of the preceding unit.
The variable 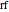 is the refinement rate (or the rate of subdivision) of the original assets. For example
is the refinement rate (or the rate of subdivision) of the original assets. For example 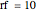 means the original unit asset is split into 10 new unit assets.
means the original unit asset is split into 10 new unit assets.
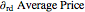 and
and 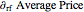 represent the sensitivity of the average price with respect to
represent the sensitivity of the average price with respect to 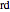 and
and 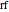 , respectively, computed as partial derivatives with respect to
, respectively, computed as partial derivatives with respect to 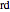 and
and 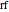 .
.
We argue that the U.S. government would discover the real price of the Troubled Assets Relief Program's (TARP) troubled assets by becoming a market maker on those assets, if those assets were purchased at a sufficiently refined level of granularity (i.e., with 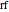 increasing).
increasing).
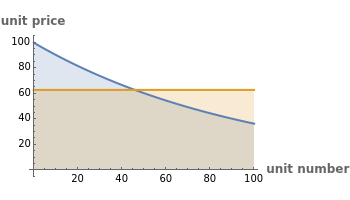
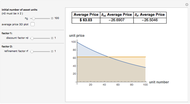
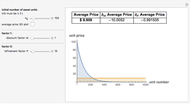
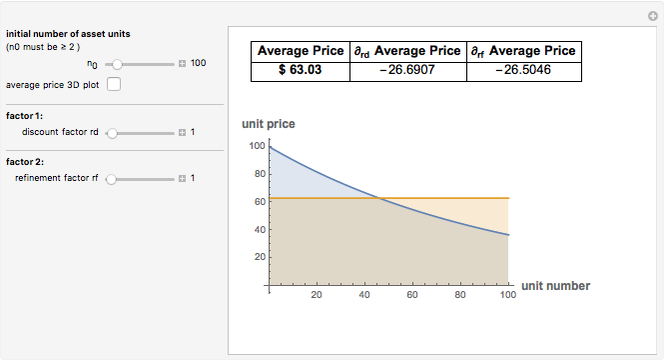
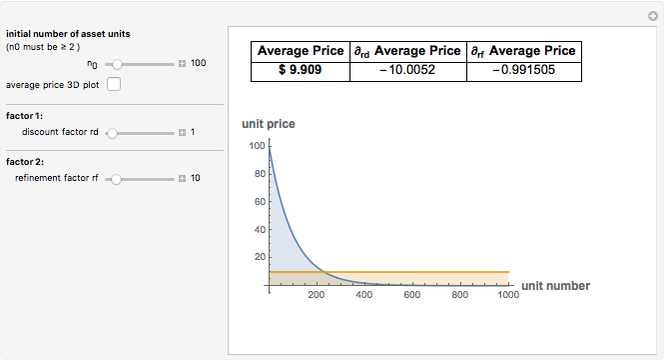
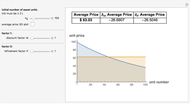
The purple line represents the average price paid for each original unit of asset as the government keeps buying units of toxic assets, assuming no additional bargain hunters enter the market.
As the discount factor 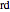 increases, the unit price decreases very quickly. But it is not desirable for the market to have a very steep discount factor, as this steepness captures a relative lack of liquidity in the market. Instead, liquidity problems can be handled by refining the unit size of the assets, which contributes to a more effective price discovery process.
increases, the unit price decreases very quickly. But it is not desirable for the market to have a very steep discount factor, as this steepness captures a relative lack of liquidity in the market. Instead, liquidity problems can be handled by refining the unit size of the assets, which contributes to a more effective price discovery process.
Furthermore, note that the sensitivity on 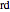 is structurally of a different order compared to the sensitivity on
is structurally of a different order compared to the sensitivity on 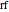 . In this simplified model, the sensitivity on
. In this simplified model, the sensitivity on 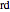 is polynomial while the sensitivity on
is polynomial while the sensitivity on 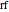 is exponential.
is exponential.
[less]

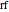 and
and 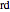 on the fair pricing of illiquid assets in a market‐making approach.
on the fair pricing of illiquid assets in a market‐making approach.