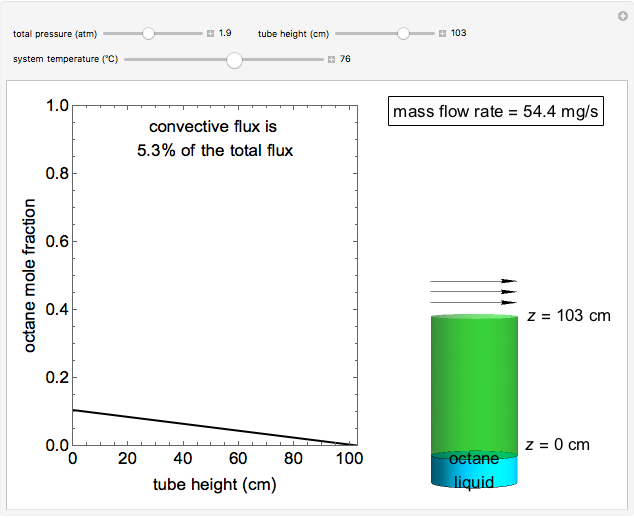
Steady-State Binary Fickian Diffusion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
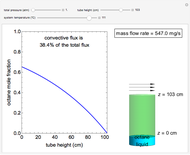
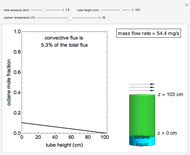
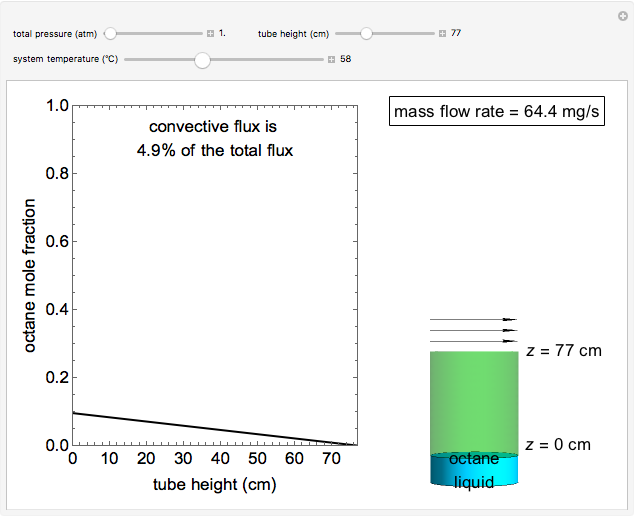
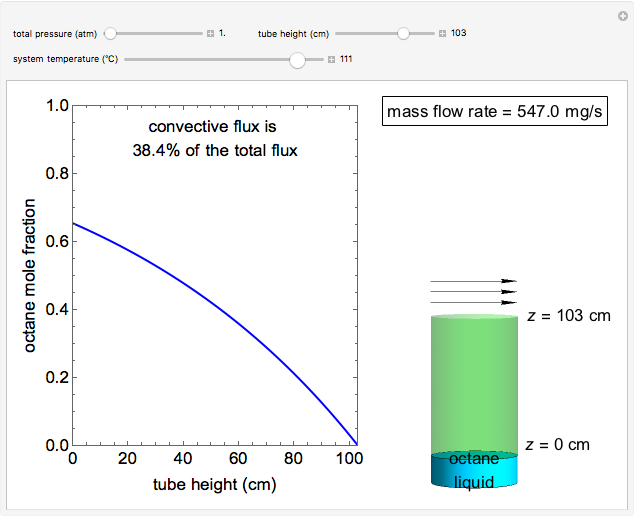
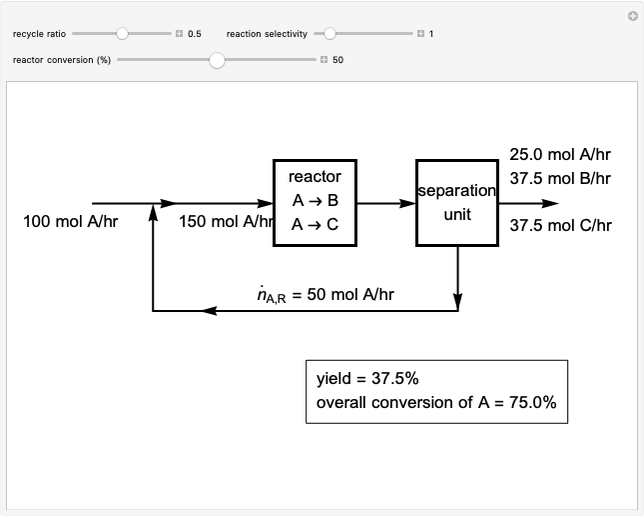
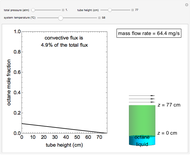
This Demonstration shows a calculation of the concentration profile and the mass flow rate of octane vapor through a tube in steady-state Fickian diffusion. Pure liquid octane is at the bottom of the vertical tube, which has a diameter of 28 cm, and a stagnant layer of air is in the tube above the liquid. Air flows across the open top of the tube to remove the octane vapor; its concentration at the top is zero. Use sliders to change the total pressure, height of the tube and temperature. The octane mole fraction versus tube height curve is shown in blue when convective flux is significant and in black when it is insignificant.
Contributed by: Muqbil Alkhalaf and Rachael L. Baumann (July 2018)
Additional contributions by: Neil Hendren and John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
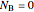 ,
,
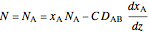 ,
,
where 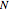 is the total flux (
is the total flux (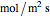 ), and
), and 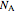 ,
,  are the fluxes of
are the fluxes of 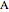 and
and 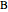 (
(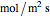 ).
).
The previous equation can be rearranged in the form of Fick's law by solving for 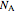 :
:
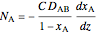 .
.
The term 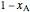 accounts for the bulk flow effect, where
accounts for the bulk flow effect, where
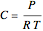 is the total molar concentration (
is the total molar concentration ( ),
),
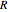 is the ideal gas constant (
is the ideal gas constant (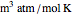 ),
),
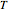 is temperature (K),
is temperature (K),
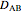 is diffusivity (
is diffusivity (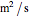 ),
),
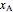 is the liquid mole fraction of
is the liquid mole fraction of 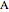
and  is the height of the tube (m).
is the height of the tube (m).
At quasi-steady state and with constant molar density, in integral form:
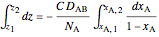 .
.
Upon integration,
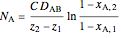 ,
,
where 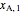 is the mole fraction at
is the mole fraction at  , and
, and 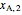 is the mole fraction at
is the mole fraction at  .
.
The mole fraction variation as a function of  is:
is:
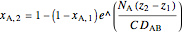 .
.
A more useful form of 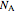 can be derived from the definition of the log mean:
can be derived from the definition of the log mean:
 .
.
Combining 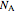 and
and 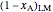 gives:
gives:
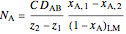 .
.
From Dalton's law, assuming equilibrium at the liquid octane/air interface:
 ,
,
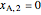 ,
,
where 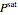 is the saturation pressure (atm).
is the saturation pressure (atm).
The saturation pressure is calculated from the Antoine equation:
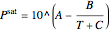 ,
,
where  ,
, 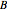 and
and 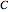 are Antoine constants.
are Antoine constants.
Solve the diffusive flux equation 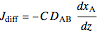 using the boundary conditions
using the boundary conditions 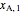 and
and 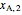 :
:
 .
.
The concentration profile is
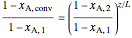 ;
;
solving for  ,
,
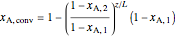 .
.
If the diffusive flux is greater than 90% of the total flux, then  .
.
Finally, the molar flow rate through the top of the tube is calculated. Given that 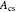 is the cross-sectional area of the tube:
is the cross-sectional area of the tube:
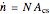 .
.
The mass flow rate is then
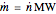 ,
,
where  is the molecular weight of the compound.
is the molecular weight of the compound.
Reference
[1] J. D. Seader, E. J. Henley and D. K. Roper, Separation Process Principles: Chemical and Biochemical Operations, 3rd ed., Hoboken, NJ: John Wiley & Sons, 2011 pp. 88–89.
Permanent Citation