Energy Balance on Pressurizing a Tank

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
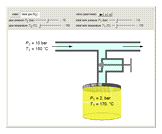
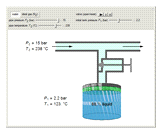
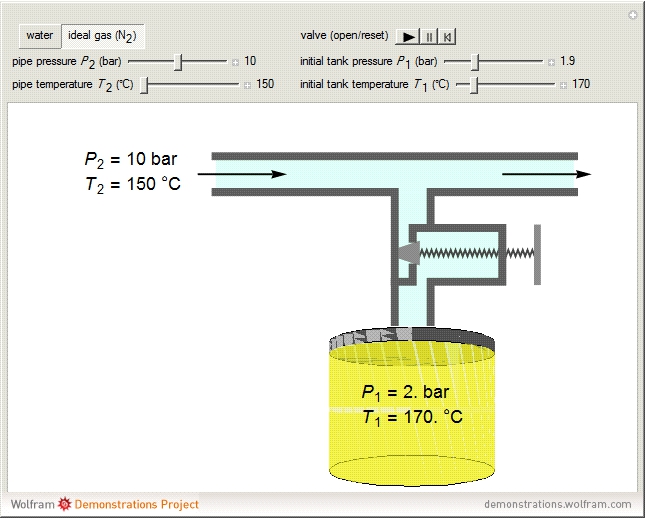
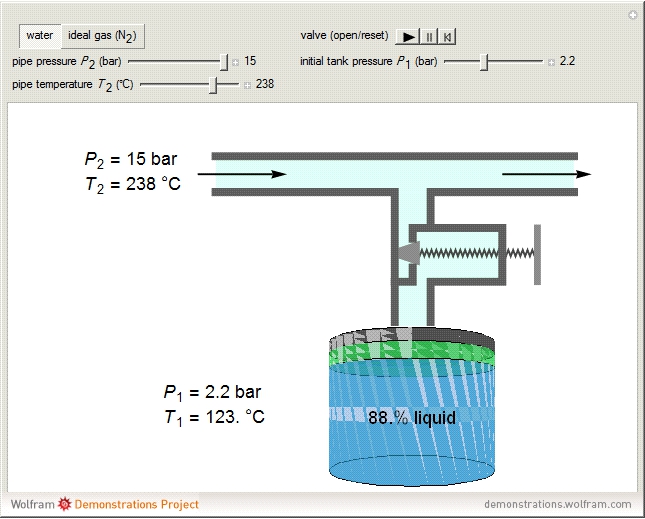
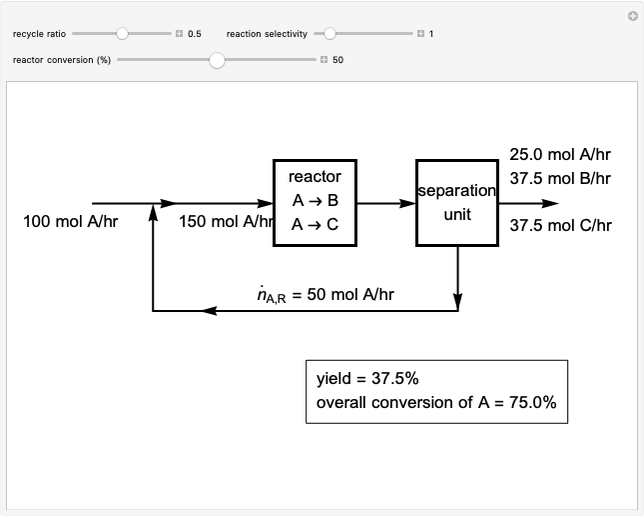
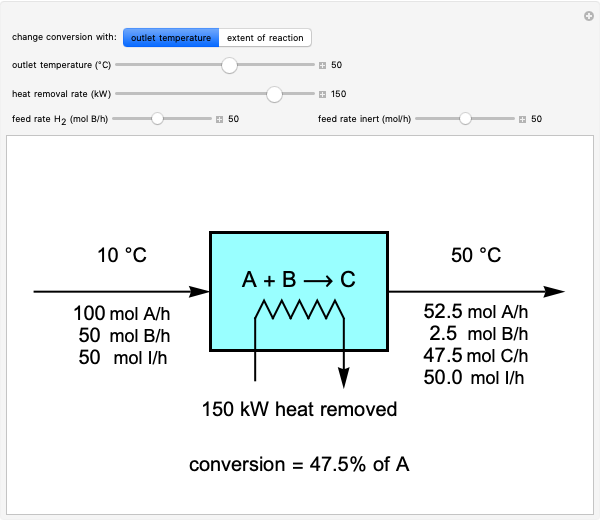
A gas flows through a pipe into an insulated tank (0.1 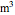 ) that is initially at a lower pressure and at a different temperature. Click the “valve (open)" play button to start gas flow into the tank; the valve closes when the pressures equalize. The tank initially contains either an ideal gas (
) that is initially at a lower pressure and at a different temperature. Click the “valve (open)" play button to start gas flow into the tank; the valve closes when the pressures equalize. The tank initially contains either an ideal gas (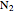 ) and more
) and more 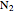 is added, or it contains a vapor-liquid mixture of water and superheated steam is added. Sliders change the pipe pressure and temperature and the initial tank pressure. The initial mass of water in the tank is 1 kg and that does not change when the initial tank pressure is changed with the slider. Initially the tank is at the saturation temperature of water at the initial pressure. Use the "valve (reset)” button to go back to the initial conditions before the valve was opened.
is added, or it contains a vapor-liquid mixture of water and superheated steam is added. Sliders change the pipe pressure and temperature and the initial tank pressure. The initial mass of water in the tank is 1 kg and that does not change when the initial tank pressure is changed with the slider. Initially the tank is at the saturation temperature of water at the initial pressure. Use the "valve (reset)” button to go back to the initial conditions before the valve was opened.
Contributed by: Rachael L. Baumann (February 2015)
Additional contributions by: John L. Falconerand Derek Machalek
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Energy Balance
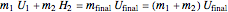 ,
,
where the subscript 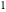 refers to what is initially inside the tank,
refers to what is initially inside the tank,  refers to what is added or in the line,
refers to what is added or in the line, 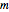 is mass (kg),
is mass (kg), 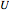 is the internal energy (kJ/kg), and
is the internal energy (kJ/kg), and 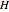 is enthalpy (kJ/kg).
is enthalpy (kJ/kg).
For a Non-Ideal System, Using Water
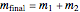 .
.
Since two phases are present in the tank at all times, the quality of the steam needs to be calculated:
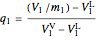 ,
,
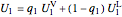 ,
,
 ,
,
where the superscripts  and
and  refer to the specific liquid and vapor properties (per kg),
refer to the specific liquid and vapor properties (per kg), 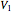 is the volume of the tank (
is the volume of the tank (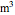 ),
), 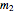 is the mass of steam added to the tank from the line, and
is the mass of steam added to the tank from the line, and 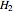 is the enthalpy at the line temperature
is the enthalpy at the line temperature 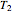 and pressure
and pressure  . The value
. The value 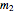 is unknown; it has to be solved for in order to evaluate the conditions of the system.
is unknown; it has to be solved for in order to evaluate the conditions of the system.
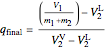 ,
,
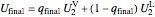 .
.
Now these expressions can be substituted into the energy balance (remember 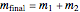 ) and solved for
) and solved for 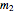 .
.
Since two phases are present in the tank, the final temperature of the system is the saturation temperature at the final pressure  .
.
For an Ideal Gas System
The number of moles 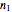 initially in the tank can be calculated using the ideal gas law:
initially in the tank can be calculated using the ideal gas law:
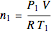 .
.
The internal energy and enthalpy are found by defining a reference point 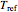 .
.
At 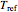 ,
, 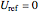 ,
,
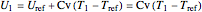 ,
,
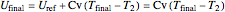 ,
,
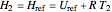 .
.
The number of moles in the tank at equilibrium 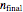 can also be calculated using the ideal gas law:
can also be calculated using the ideal gas law:
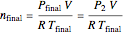 .
.
This equation can be substituted into the energy balance to solve for the final temperature 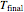 .
.
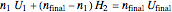 .
.
The subscript 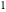 refers to the gas in the tank before more gas is added, the subscript
refers to the gas in the tank before more gas is added, the subscript  refers to the gas in the line, the subscript
refers to the gas in the line, the subscript 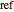 denotes a reference state,
denotes a reference state,  is pressure (bar),
is pressure (bar), 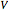 is volume (L),
is volume (L),  is the ideal gas constant ([L bar]/[mol K]),
is the ideal gas constant ([L bar]/[mol K]), 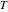 is temperature (°C),
is temperature (°C), 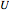 is internal energy (J/mol),
is internal energy (J/mol), 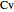 is the constant-volume heat capacity for an ideal gas (J/[mol K]), and
is the constant-volume heat capacity for an ideal gas (J/[mol K]), and 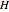 is enthalpy (J/mol).
is enthalpy (J/mol).
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Energy Balance on Pressurizing a Tank. www.colorado.edu/learncheme/thermodynamics/EnergyBalancePressurizingTank.html.
Permanent Citation