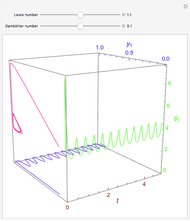
Multiple Steady States in a Continuous Stirred-Tank Reactor with Heat Exchange

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
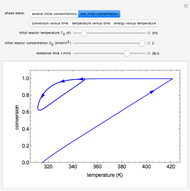
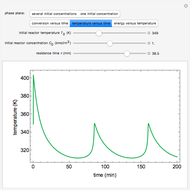
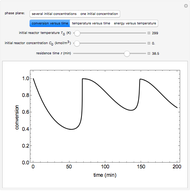
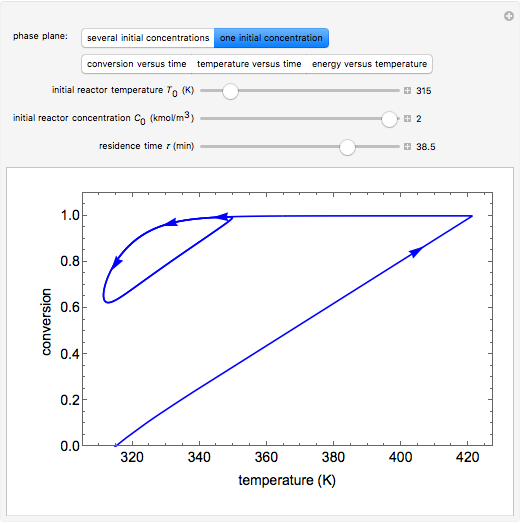
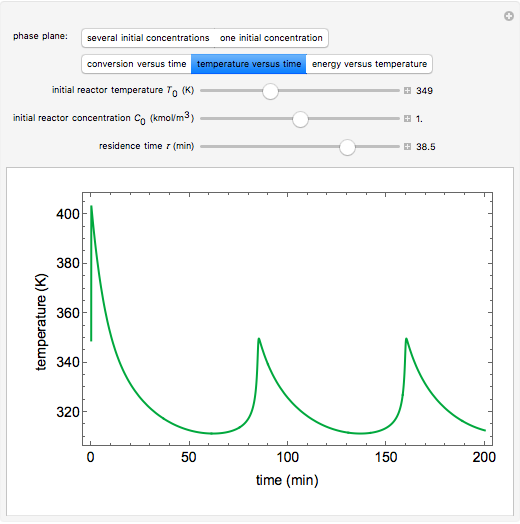
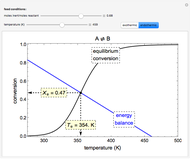
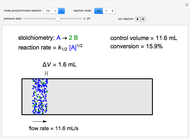
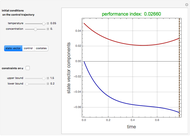
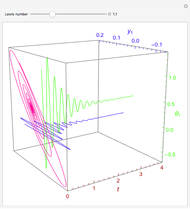
A continuous stirred-tank reactor (CSTR) with heat exchange is used for an exothermic reaction. Multiple steady-state solutions are observed; they can be stable, unstable, or exhibit sustained oscillations (limit cycles). The steady-state operating conditions depend on initial conditions (CSTR start up) and on the residence time, and limit-cycle behavior is observed for residence times greater than about 30 minutes. Select "phase plane 1" to plot reactant concentration versus reactor temperature for five initial concentrations; change the initial reactor temperature with a slider. Select "phase plane 2" to plot conversion versus temperature for one initial condition; set the initial reactor temperature and initial reactant concentration with sliders. The reactant feed concentration is 2  and the feed temperature is 298 K. In both plots, the arrows indicate the direction of time. Set the initial conditions with sliders for "phase plane 2", "temperature vs. time" and "conversion vs. time" plots; these show how a steady state (or a limit cycle) is approached. Select "energy vs. temperature" to plot heat generated and heat removed versus temperature; the intersections of the straight blue line and green curve correspond to steady-state solutions to the mass and energy balances for the CSTR. The heat transfer fluid is at a constant temperature of 300 K.
and the feed temperature is 298 K. In both plots, the arrows indicate the direction of time. Set the initial conditions with sliders for "phase plane 2", "temperature vs. time" and "conversion vs. time" plots; these show how a steady state (or a limit cycle) is approached. Select "energy vs. temperature" to plot heat generated and heat removed versus temperature; the intersections of the straight blue line and green curve correspond to steady-state solutions to the mass and energy balances for the CSTR. The heat transfer fluid is at a constant temperature of 300 K.
Contributed by: Rachael L. Baumann (January 2014)
With additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Mole balance:
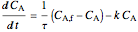 ,
,
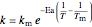 ,
,
where  is the concentration of reactant
is the concentration of reactant 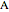 (
( ),
),  is the feed concentration of
is the feed concentration of 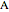 (
( ),
),  is time (min),
is time (min),  is residence time (min),
is residence time (min),  is the rate constant (1/min),
is the rate constant (1/min),  is the rate constant at mean temperature
is the rate constant at mean temperature  (1/min),
(1/min),  is reactor temperature (K), and
is reactor temperature (K), and  is activation energy (kJ/kmol).
is activation energy (kJ/kmol).
Energy balance:
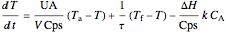 ,
,
where 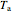 and
and 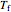 are the heat transfer fluid and feed temperatures (K),
are the heat transfer fluid and feed temperatures (K),  is the overall heat transfer coefficient times heat transfer area (kJ/[min K]),
is the overall heat transfer coefficient times heat transfer area (kJ/[min K]),  is reactor volume (
is reactor volume ( ),
), 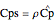 is specific heat capacity (
is specific heat capacity ( ),
),  is density of reactants (
is density of reactants ( ),
),  is average heat capacity of reactants (kJ/[kg K]), and
is average heat capacity of reactants (kJ/[kg K]), and  is heat of reaction (kJ/kmol).
is heat of reaction (kJ/kmol).
The heats generated 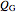 and removed
and removed  are:
are:
 ,
,
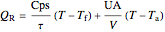 ,
,
where 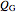 and
and  are in units of (
are in units of (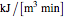 ).
).
Conversion of reactant  is:
is:
 .
.
The screencast video at [2] explains how to use this Demonstration.
References
[1] J. G. Ekerdt and J. B. Rawlings, Chemical Reactor Analysis and Design Fundamentals, Madison, WI: Nob Hill Publishing, 2002 pp. 296–316.
[2] Multiple Steady States in a Continuous Stirred-Tank Reactor with Heat Exchange. www.colorado.edu/learncheme/kinetics/MultipleSteadyStatesCSTR.html.
Permanent Citation