Sum of Medians Divided by the Perimeter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
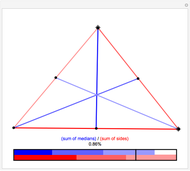
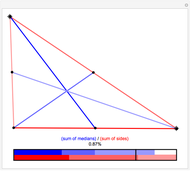
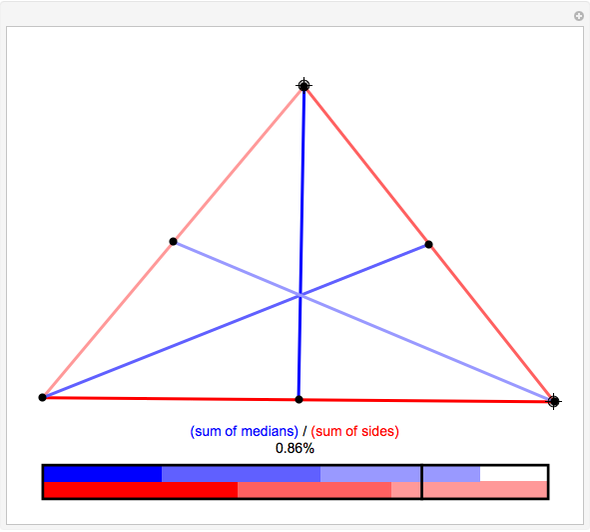
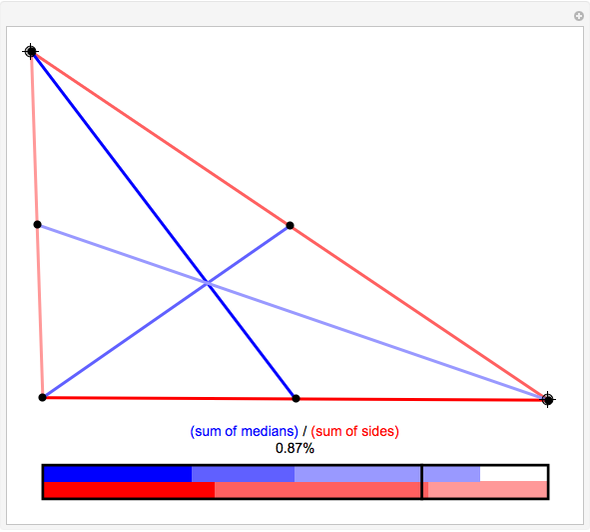
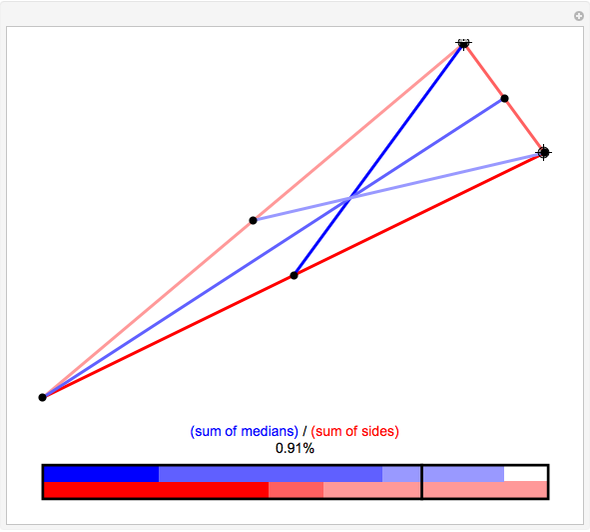
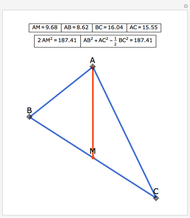
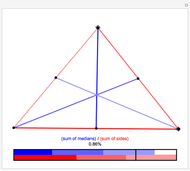
It is a simple theorem that the sum of the lengths of the medians in a triangle must be between  and
and  , where
, where  is the perimeter of the triangle. By dragging the vertices of the triangle, you can confirm the theorem and discover which kinds of triangles come close to achieving the lower and upper bounds of 75% and 100% of the perimeter, respectively.
is the perimeter of the triangle. By dragging the vertices of the triangle, you can confirm the theorem and discover which kinds of triangles come close to achieving the lower and upper bounds of 75% and 100% of the perimeter, respectively.
Contributed by: Jacob A. Siehler (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] H. S. M. Coxeter, Introduction to Geometry, New York: John Wiley & Sons, 1961.
[2] "Medians of Triangles Proof" from The Math Forum: Ask Dr. Math. (May 29, 2000) mathforum.org/library/drmath/view/55242.html.
Permanent Citation
"Sum of Medians Divided by the Perimeter"
http://demonstrations.wolfram.com/SumOfMediansDividedByThePerimeter/
Wolfram Demonstrations Project
Published: December 18 2012