Conway's M(13) Puzzle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
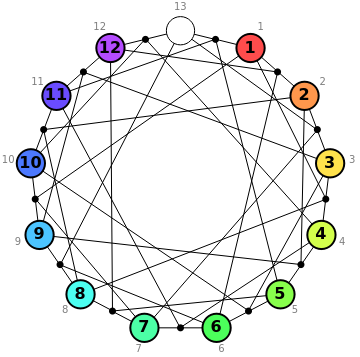
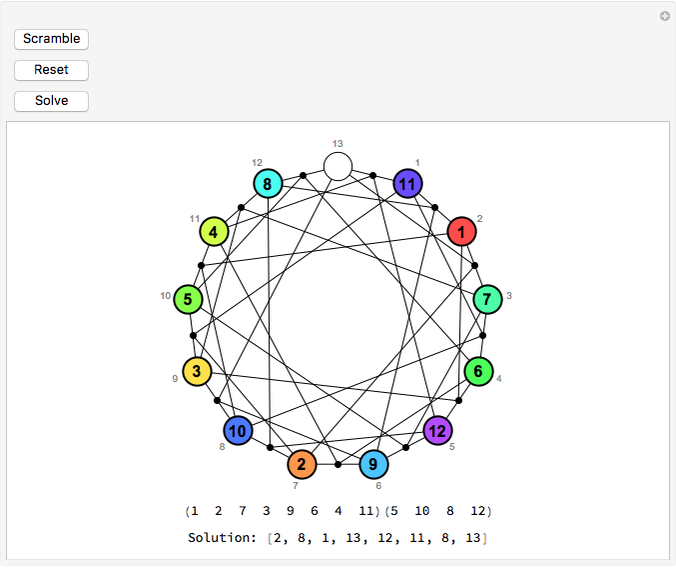
John H. Conway introduced this sliding tile puzzle, which bears the same relation to the Mathieu group 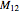 as Sam Lloyd's famous 15 puzzle bears to the alternating group
as Sam Lloyd's famous 15 puzzle bears to the alternating group 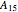 . (
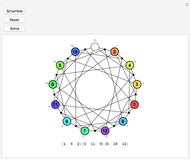
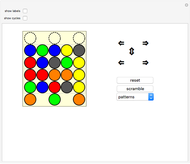
. (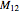 was one of the first sporadic simple groups to be discovered.) Initially, tiles numbered 1–12 are placed on the same-numbered points of a projective plane of order three, with the
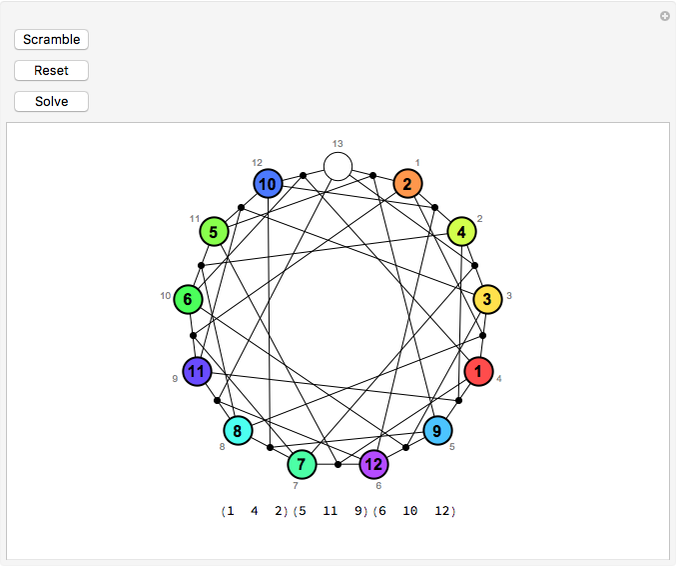
was one of the first sporadic simple groups to be discovered.) Initially, tiles numbered 1–12 are placed on the same-numbered points of a projective plane of order three, with the  point left uncovered. Hovering over a tile reveals the four points in the unique line of the projective plane that connects it to the uncovered point. Clicking the tile executes the sole legal move of the game, which is a double transposition: the clicked tile slides in to the uncovered space, and the other two points on the line exchange positions. The object, of course, is to restore the tiles to their initial order from a scrambled position.
point left uncovered. Hovering over a tile reveals the four points in the unique line of the projective plane that connects it to the uncovered point. Clicking the tile executes the sole legal move of the game, which is a double transposition: the clicked tile slides in to the uncovered space, and the other two points on the line exchange positions. The object, of course, is to restore the tiles to their initial order from a scrambled position.
Contributed by: Jacob A. Siehler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The M(13) in the title refers to the pseudogroup of permutations of the 13 tiles (where we think of the open space as simply another tile bearing the number 13) that can be achieved by legal moves in the game. The subset of permutations that leave the  point uncovered form a group of 95,040 elements ismorphic to the Mathieu group
point uncovered form a group of 95,040 elements ismorphic to the Mathieu group 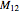 .
.
The solver is based on the algorithm described in the following paper (which would be impractical for a human puzzler to use):
J. H. Conway, N. D. Elkies, and J. L. Martin, "The Mathieu Group 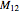 and Its Pseudo Group Extension
and Its Pseudo Group Extension  ," Experimental Mathematics, 15(2), 2006 pp. 223–236. [PDF]
," Experimental Mathematics, 15(2), 2006 pp. 223–236. [PDF]
Permanent Citation