Wolfram Research

Mathematica MathWorld Wolfram Science More »

The Sum of the Perimeters of Three Subtriangles


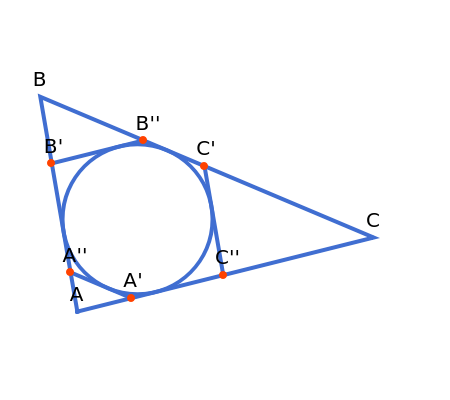
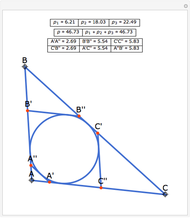
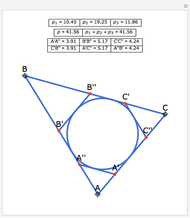
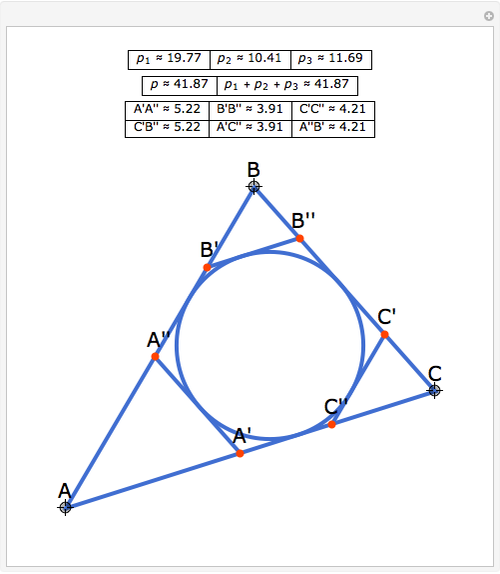
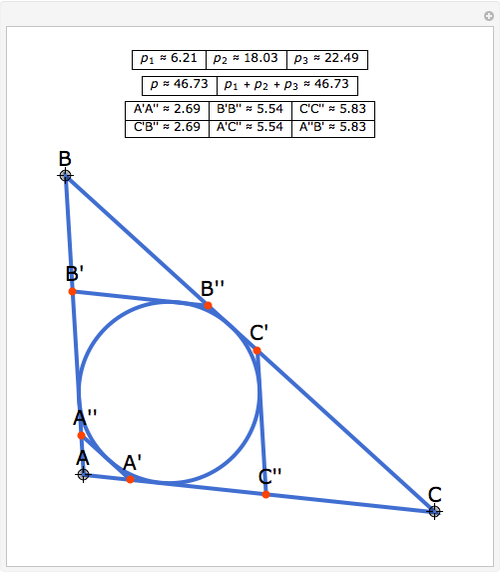
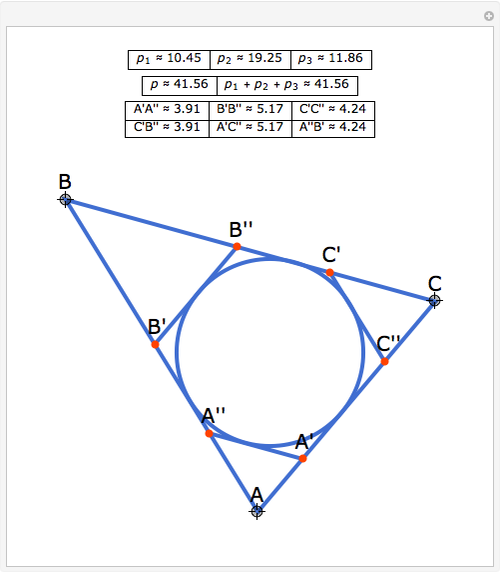
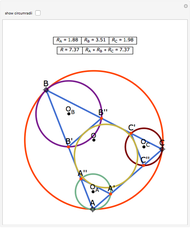
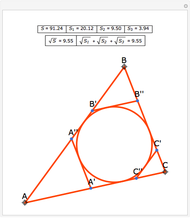
	Let ABC be a triangle. Let A'A'', B'B'', and C'C'' be tangents to the incircle of ABC and parallel to BC, AC, and AB, respectively. Let 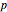be the perimeter of ABC 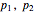and , and 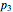be the perimeters of AA'A'', BB'B'', and CC'C'', respectively. Then 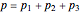. Also, opposite sides of the hexagon A'A''B'B''C'C'' are equal, that is, A'A'' = C'B'', B'B'' = A'C'', and C'C'' = A''B'.


	Contributed by: Jay Warendorff After work by: Antonio Gutierrez

The statement of the theorem is in Problem 141. Triangle, Incircle, Tangent and parallel to side, Perimeter.

Incircle (Wolfram MathWorld)

Parallel (Wolfram MathWorld)

Parallel Lines (Wolfram MathWorld)

Perimeter (Wolfram MathWorld)

"The Sum of the Perimeters of Three Subtriangles" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/TheSumOfThePerimetersOfThreeSubtriangles/

Contributed by: Jay Warendorff

After work by: Antonio Gutierrez

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Related Topics

Browse all topics

Some Related Demonstrations

Share & Bookmark This Demonstration

Contribute

Powered by Wolfram Mathematica

Give us your feedback

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

© 2009 Wolfram Demonstrations Project & Contributors

Wolfram Research

Site Index

RSS

Atom

Note: To run this Demonstration you need the free
Mathematica Player or Mathematica 7+