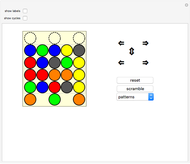
Sylver Coinage is a game invented by J. H. Conway in which players take turns choosing positive integers—but a player may only choose an integer that cannot be expressed as a sum of positive multiples of integers already chosen. The player who is forced to choose “1” loses the game. The name of the game is a nod to J. J. Sylvester, who proved that is the largest sum that cannot be paid exactly using coins of value and , if and are relatively prime. Gameplay is simple: just click the value you want to "coin", and illegal moves will be removed from the board automatically. Finding a winning strategy may not be so simple, however.