Ten Billion Barrel Puzzle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
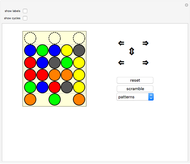
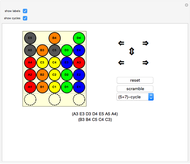
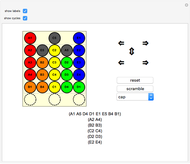
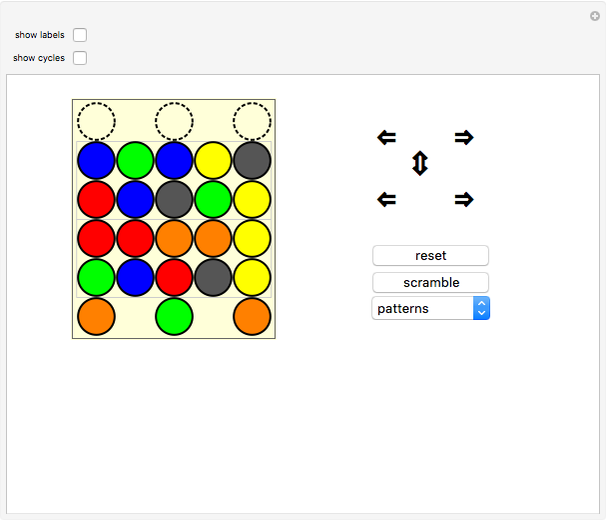
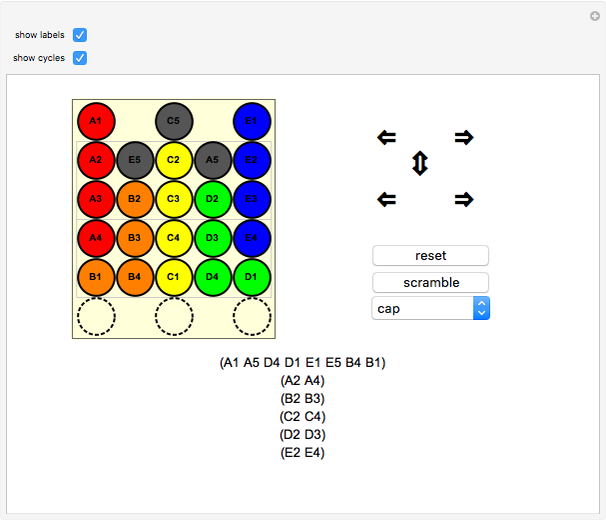
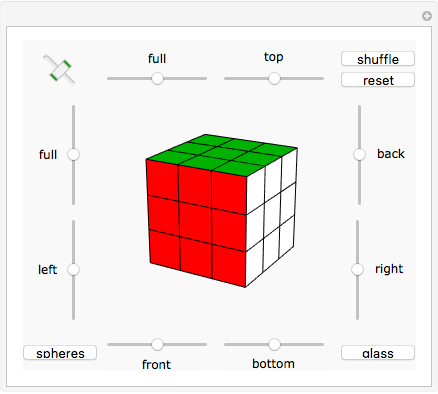
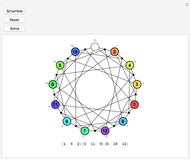
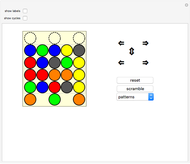
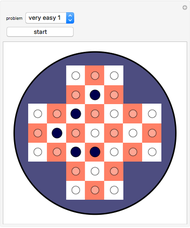
A simulation of Nintendo's Ten Billion Barrel puzzle. Click on the arrows to rotate the rings of beads left and right, or to shift the columns up and down. You can try to restore the puzzle to its pristine state from a scrambled position, and try to solve (or reproduce) any of the "pretty patterns" provided. When the beads are labeled, all 23!/2 even permutations of the beads can be achieved, and you can show the current permutation of the beads in disjoint cycle form. The first few patterns in the dropdown menu are useful algorithms to learn for solving arbitrary positions of the puzzle—if you can solve those, you can (with patience) solve anything.
Contributed by: Jacob A. Siehler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This puzzle was designed by Gunpei Yokoiand originally appeared in 1980. The physical puzzle consists of five rotating rings of beads in a clear plastic cylinder with a plunger mechanism that shifts three of the columns up and down. Counting the number of positions that can be achieved requires some clarification: as mentioned above, all 23!/2 (approximately 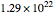 ) even permutations of the beads can be achieved, but in the physical puzzle, beads of a given color are indistinguishable, so a more realistic count would reduce that by a factor of
) even permutations of the beads can be achieved, but in the physical puzzle, beads of a given color are indistinguishable, so a more realistic count would reduce that by a factor of 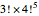 , leaving approximately
, leaving approximately  visually distinct states. Since an odd permutation of the beads can be changed to an even permutation by transposing a pair of indistinguishable beads, any desired arrangement of colors can be achieved in the puzzle when labels are turned off. One further twist: the physical puzzle is symmetric top-to-bottom, and can be turned upside down to effect an odd permutation of the beads (hence making all permutations of the beads possible).
visually distinct states. Since an odd permutation of the beads can be changed to an even permutation by transposing a pair of indistinguishable beads, any desired arrangement of colors can be achieved in the puzzle when labels are turned off. One further twist: the physical puzzle is symmetric top-to-bottom, and can be turned upside down to effect an odd permutation of the beads (hence making all permutations of the beads possible).
More information, including several algorithms for solving the puzzle, can be found at Jaap Scherphuis's ten billion barrel page, which is also the source for several of the pretty patterns provided here.
Permanent Citation