MAX Puzzle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
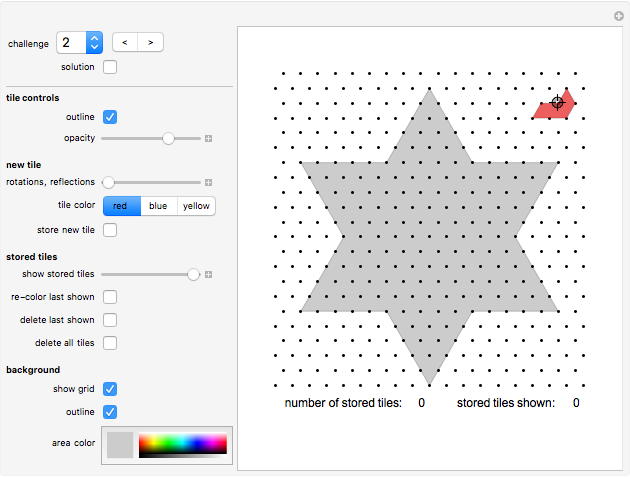
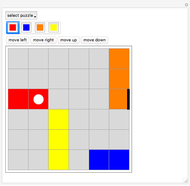
The MAX Puzzle asks you to fill shapes with congruent copies of the MAX tile shown at the top right corner.
[more]
Contributed by: Karl Scherer (May 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
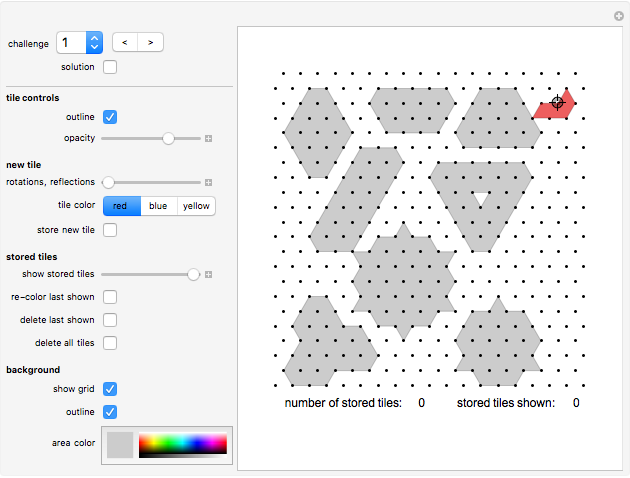
Controls
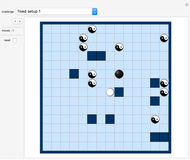
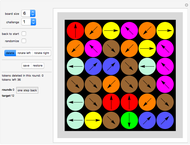
The "challenge" popup-menu shows you various shapes to fill. Use the "<,>" buttons to page forwards and backwards. Challenge 10 is an empty board for free play.
The "solution" button works only for challenge 8, 9 and 10; see details below.
You draw a tile by a stamping method: Move the sample tile with the Locator (which initially is positioned at the top right corner) to the desired position on the board. Click one of the three color buttons to select its color. Use the "rotations, reflections" slider to select the orientation of the tile. Now click the "store new tile" button. The new tile will be displayed from now on. You can now use the Locator-tile to stamp the next tile.
Using the "show stored tiles" slider to display only some of the placed tiles.
After selecting "show stored tiles", click "re-color last shown" to change the coloring of a placed tile.
After selecting "show stored tiles", click "delete last shown" button to delete the tile that was shown last.
Click "delete all tile" to clear the board.
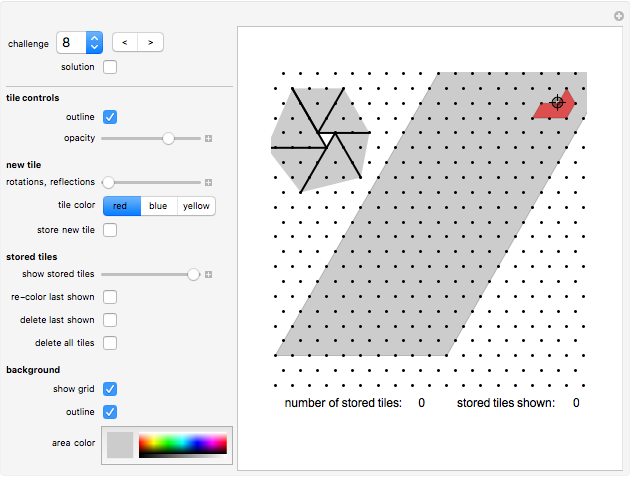
Challenge 8
In challenge 8 and 9 you are asked to fill areas of infinite size. These two challenges are the only ones with a proper solution given (click the "solution" button to see it).
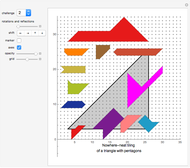
If we call this area a "strip", then we can join (horizontally) an infinite number of such strips to cover a 60-degrees wedge of the plane.
The little diagram shows how we can then combine two such wedges to fill a 120-degrees wedge. Then we can combine three such 120-degrees wedges to fill the while plane, but we can also combine three such 120-degrees wedges in a way such that a small regular triangle stays uncovered. In a similar we can combine six 60-degrees wedges so that the area of a regular hexagon (with unit side-length) stays uncovered.
Challenge 9
An infinite area with a blunted corner is given. This is a bit harder problem that challenge 8. If you click the "solution" button, you get a solution which can be extended infinitely far (just add more blue and green areas).
We can add the 60°-wedge from challenge 8 to get a covering of the blunted 60° wedge of the plane.
Six copies of these extended blunted 60°-wedges can be joint to cover the whole plane minus one regular hexagon, giving us a second solution to the problem "Can we start with regular hexagon and tile the rest of the plane such that the tiling has six-fold rotational symmetry?"
Challenge 10
An infinite area with a blunted corner is given. If you click the "solution" button, you get a solution which can be extended infinitely far (just add more blue and green areas). You can also place copies of this infinite tiling next to each other to the right of the original to obtain a blunted 60°-wedge in a very simple way (compare this this to challenges 8 and 9).
History
The MAX Puzzle was invented by the author of this Demonstration in 1987 and implemented as a Zillions game in November 2000.
The task is to fill shapes with congruent copies of the MAX tile shown at the top right corner. The author has collected more than 200 interesting shapes that can be tiled with MAX tiles, of which only a small selection are presented here.
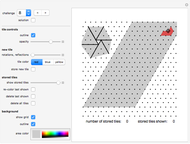
Using the six-pointed star (challenge 2) as a playing board, he also developed a 2-player game. The rules are:
Each player uses only one color. You win if you either connect two tips of the star or, if no player manages to connect tips, create the longest "fence" consisting of connected tiles of your color.
Permanent Citation
"MAX Puzzle"
http://demonstrations.wolfram.com/MAXPuzzle/
Wolfram Demonstrations Project
Published: May 5 2008