Wolfram Research

Mathematica MathWorld Wolfram Science More »

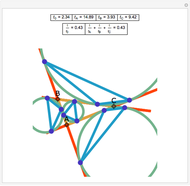
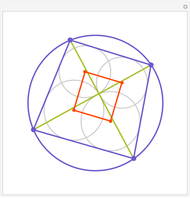
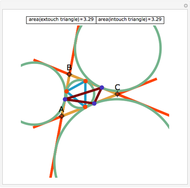
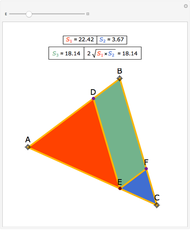
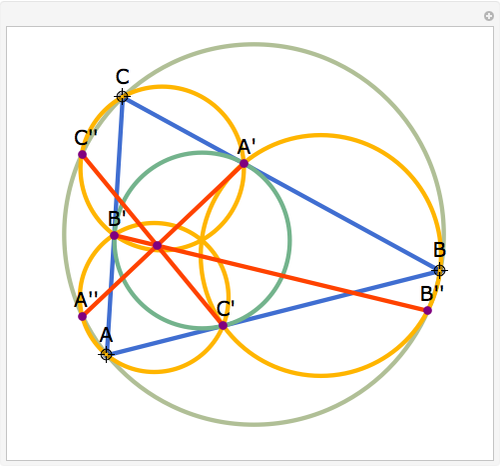
The Contact Triangle and Two Other Subtriangles


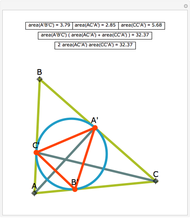
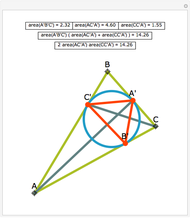
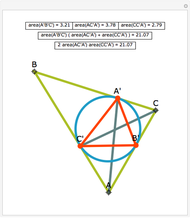
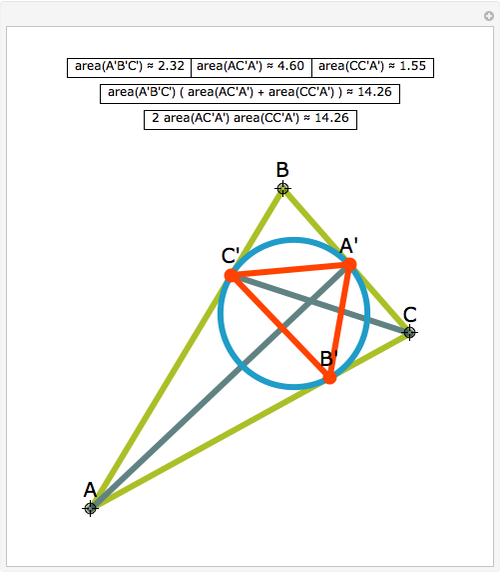
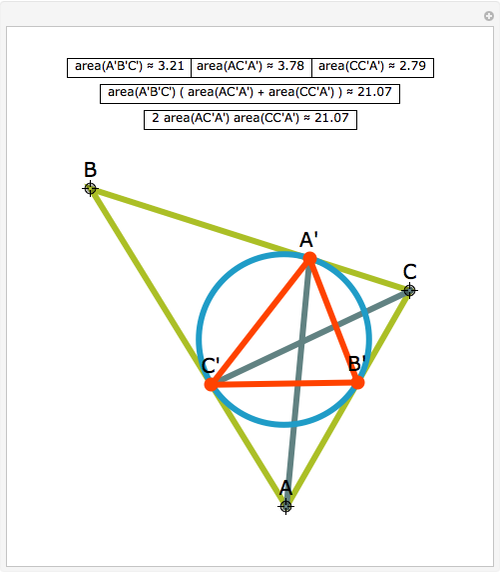
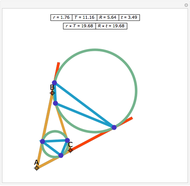
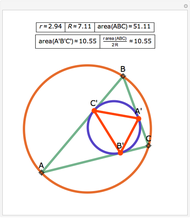
	Let ABC be a triangle. Let A', B', and C' be the vertices of the contact triangle (the triangle with vertices where the incircle touches the sides of ABC). If 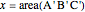, , 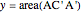and 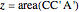, then .


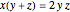	Contributed by: Jay Warendorff After work by: Antonio Gutierrez

The statement of the theorem is in Problem 110. Contact Triangle, Area, Incircle.

Contact Triangle (Wolfram MathWorld)

Incircle (Wolfram MathWorld)

"The Contact Triangle and Two Other Subtriangles" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/TheContactTriangleAndTwoOtherSubtriangles/

Contributed by: Jay Warendorff

After work by: Antonio Gutierrez

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Related Topics

Browse all topics

Some Related Demonstrations

Share & Bookmark This Demonstration

Contribute

Powered by Wolfram Mathematica

Give us your feedback

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

© 2009 Wolfram Demonstrations Project & Contributors

Wolfram Research

Site Index

RSS

Atom

Note: To run this Demonstration you need the free
Mathematica Player or Mathematica 7+