The Eigenvectors of a Random Graph

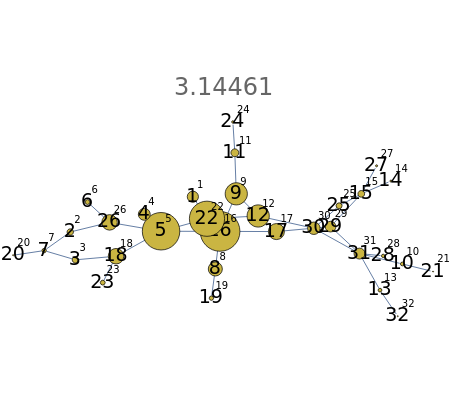
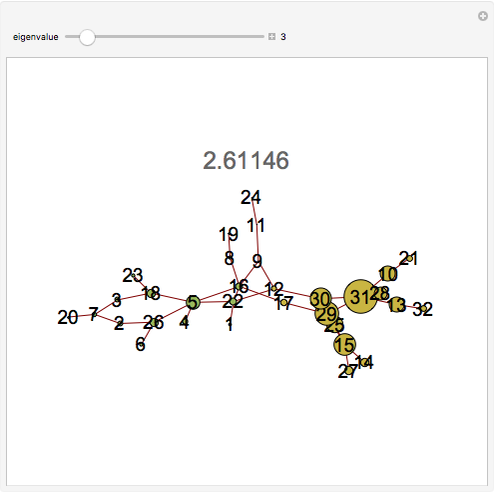
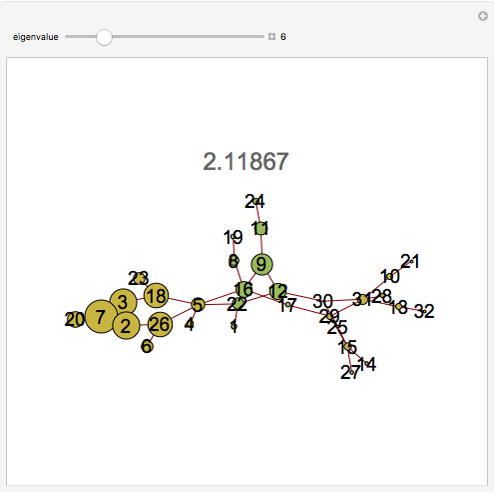
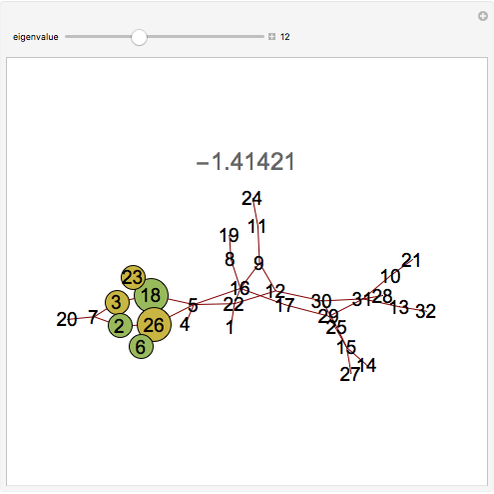
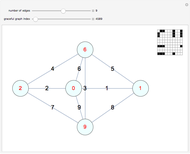
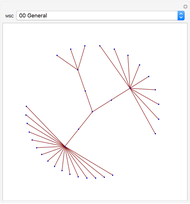
A graph can be represented by an adjacency matrix, with an entry of 1 at position if the node is connected to the node, and 0 otherwise. This Demonstration provides a visualization of the eigenvectors of the adjacency matrix of a graph. The eigenvalue is indicated above the graph. The size of the nodes (circles) are proportional to the absolute magnitude of that component of the eigenvector; the eigenvectors are related to the problem of graph partitioning. Yellow nodes indicate positive values and green nodes indicate negative values. The relative sizes of the nodes for a given eigenvalue indicate the relative importance (ranking of those nodes) as well as the community structure of the graph.