Topological Sort in DAGs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A topological sort (or topological ordering) of a directed graph is a linear ordering of its vertices such that for every edge 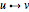 ,
,  comes before
comes before  in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges
in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges 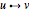 may represent constraints that one task
may represent constraints that one task  must be performed before another
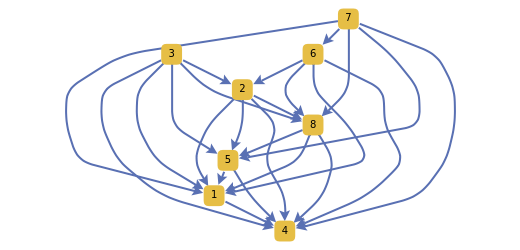
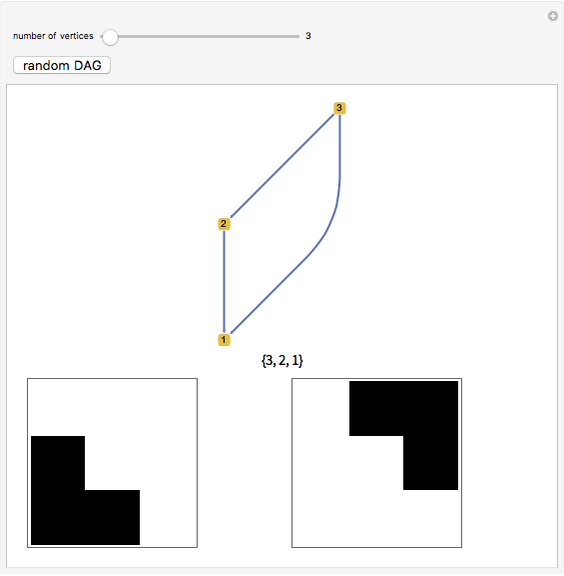
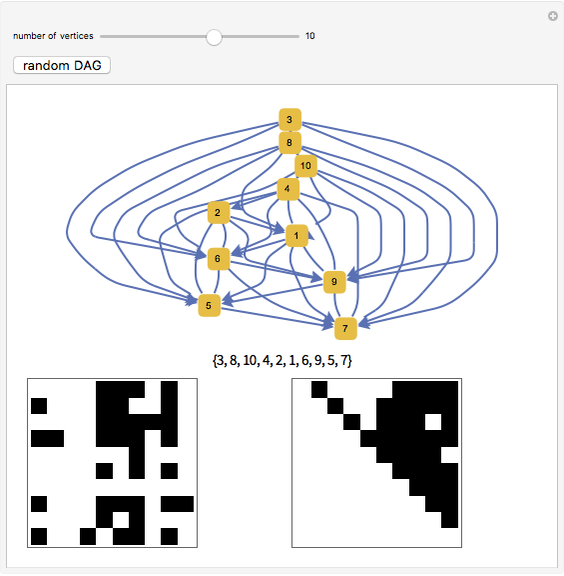
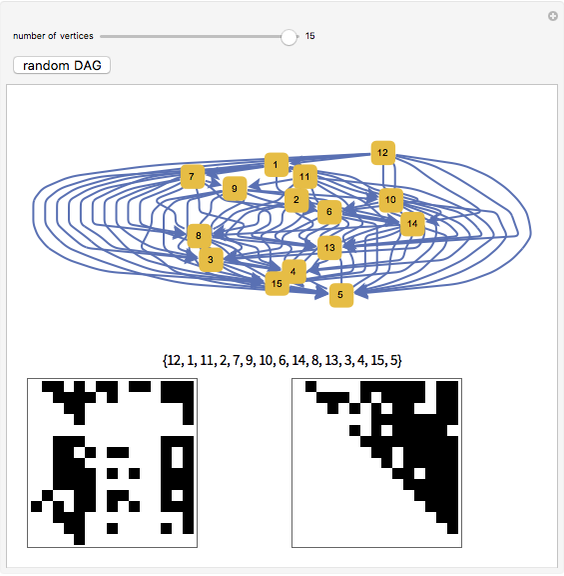
must be performed before another  . In this application, a topological ordering is just a valid sequence of tasks. A topological ordering is possible only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. This Demonstration shows random DAGs with a prescribed number of vertices along with one topological sort and two matrices. The matrix on the left represents the adjacency matrix of the graph. In the first graph, vertices 2, 3, and 5 have no out vertices; for that reason their rows are empty. The matrix on the right shows the adjacency matrix corresponding to a relabeling of the vertices following the topological sort; this matrix is upper triangular.
. In this application, a topological ordering is just a valid sequence of tasks. A topological ordering is possible only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. This Demonstration shows random DAGs with a prescribed number of vertices along with one topological sort and two matrices. The matrix on the left represents the adjacency matrix of the graph. In the first graph, vertices 2, 3, and 5 have no out vertices; for that reason their rows are empty. The matrix on the right shows the adjacency matrix corresponding to a relabeling of the vertices following the topological sort; this matrix is upper triangular.
Contributed by: Jaime Rangel-Mondragon (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Topological Sort in DAGs"
http://demonstrations.wolfram.com/TopologicalSortInDAGs/
Wolfram Demonstrations Project
Published: August 23 2011