navbar-top.gif
btn_spacer.gifHomeTopicsLatestRandomAboutFAQsParticipateAuthoring Areabtn_spacer.gif

Eigenvalues of Random Symmetric Matrices
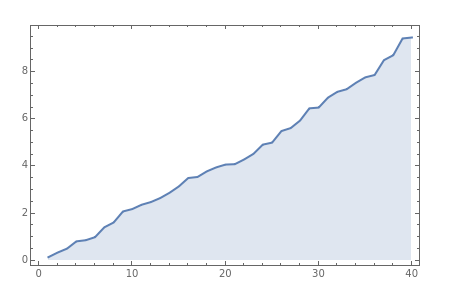
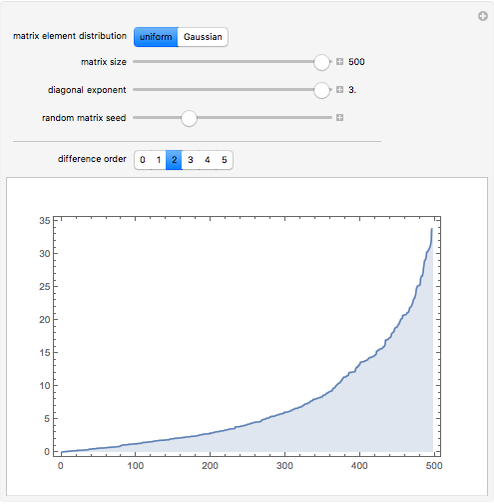
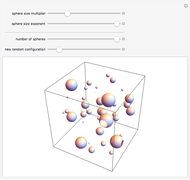
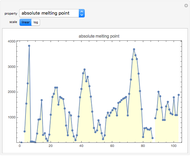
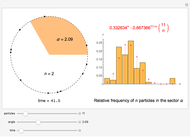
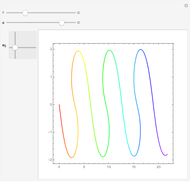
Watch how the eigenvalues of random symmetric matrices approach a universal distribution as the size of the matrix increases.



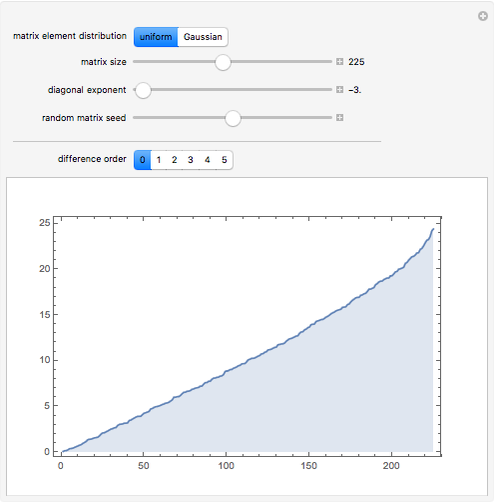
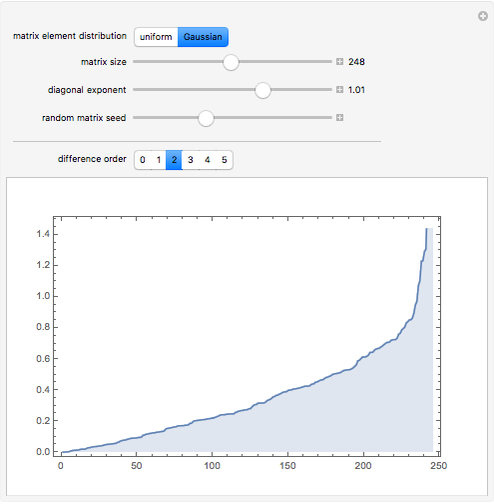
The eigenvalues (or their differences) are sorted, and plotted in sequence.
With diagonal exponent 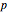, the constant 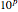is added to each element on the diagonal.


"Eigenvalues of Random Symmetric Matrices" from The Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/EigenvaluesOfRandomSymmetricMatrices/
Contributed by: Stephen Wolfram and Michael Trott
Powered by Wolfram Mathematica
Give us your feedback
Give us your feedback

Source page:




 often  occasionally  never

Note: Please do not include anything you consider confidential or proprietary. We will keep your information private. We will not give it to any third party.
Privacy Policy »
©  2008 The Wolfram Demonstrations Project & Contributors    Wolfram Research    Site Index    Terms of Use    Privacy Policy    RSS    Atom