Geodesics and Conjugate Loci on a Torus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
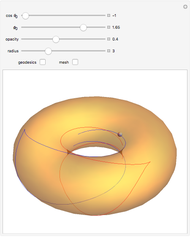
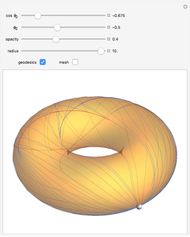
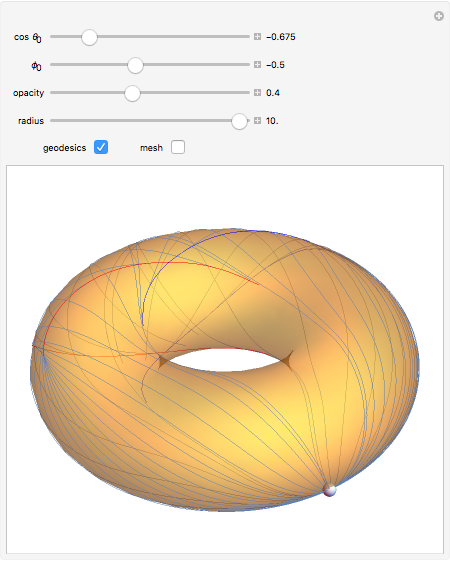
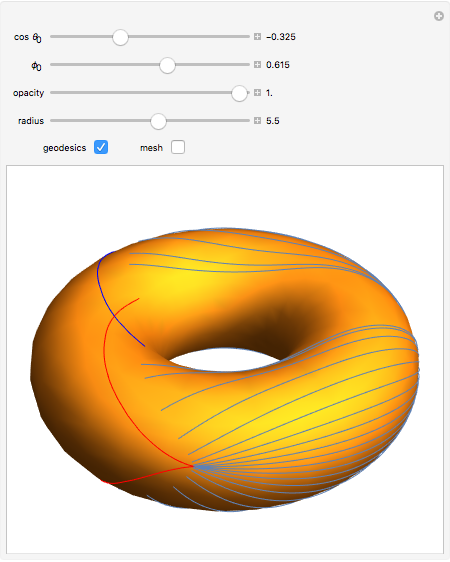
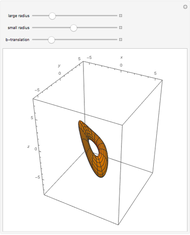
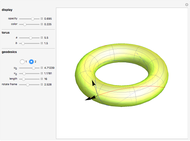
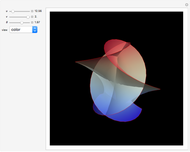
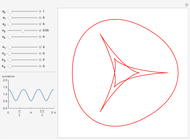
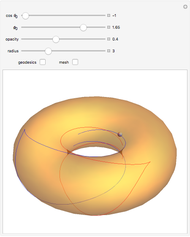
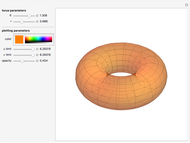
Geodesics moving across a surface may focus due to the curvature of the surface. The set of geodesics emanating from a "base point" (the small sphere) on the surface of a torus can focus along a curve called the conjugate locus. This Demonstration explores several possible cases of conjugate loci on the standard torus.
Contributed by: Matthew Cherrie and Thomas Waters (October 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The base point from which the geodesics emanate is shown by a small sphere that you can move on the torus by varying  and
and  (standard coordinates are used;
(standard coordinates are used; 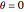 and
and 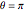 correspond to the outer and inner equators, respectively). Two sets of geodesics are shown and plotted for a length given by "radius." The Jacobi equation is solved along each geodesic until the conjugate point is reached. The component of the conjugate locus due to each set is shown as either a heavy red or blue curve.
correspond to the outer and inner equators, respectively). Two sets of geodesics are shown and plotted for a length given by "radius." The Jacobi equation is solved along each geodesic until the conjugate point is reached. The component of the conjugate locus due to each set is shown as either a heavy red or blue curve.
As geodesics tend toward the inner equator, the conjugate points get further away and the resulting geodesic plotted on the torus can cloud the picture, so you can switch the geodesics on or off.
Reference
[1] M. L. Irons, "The Geodesics of the Torus," (Oct 5, 2016) www.rdrop.com/~half/math/torus/geodesics.xhtml.
Permanent Citation
"Geodesics and Conjugate Loci on a Torus"
http://demonstrations.wolfram.com/GeodesicsAndConjugateLociOnATorus/
Wolfram Demonstrations Project
Published: October 6 2016