Details

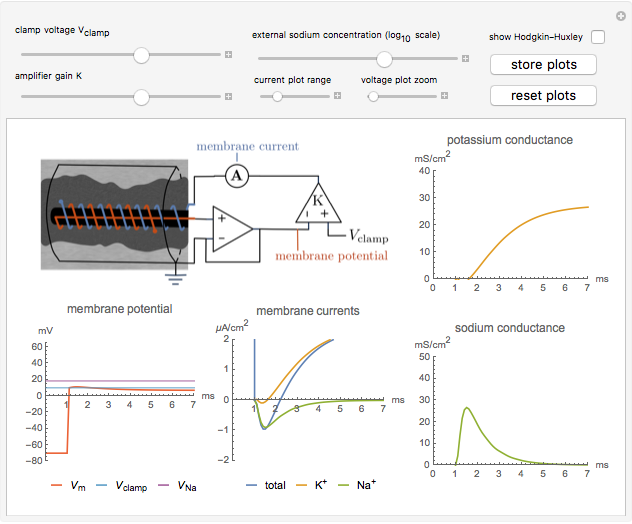
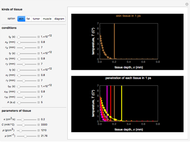
Snapshot 1: the sodium and potassium conductances can be determined following the experimental procedure of Hodgkin, Huxley, and Katz

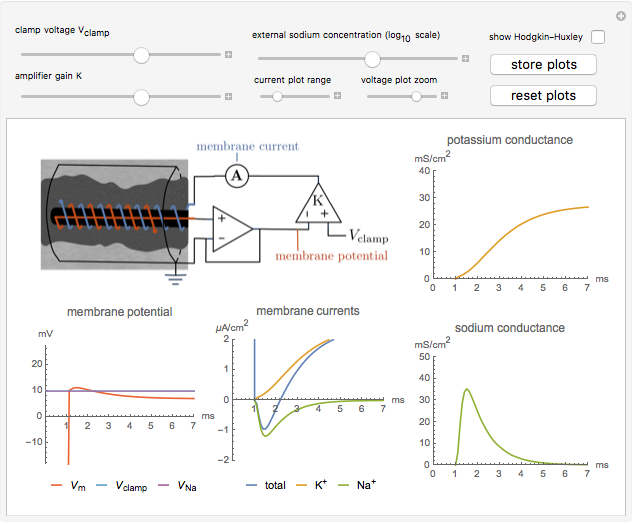
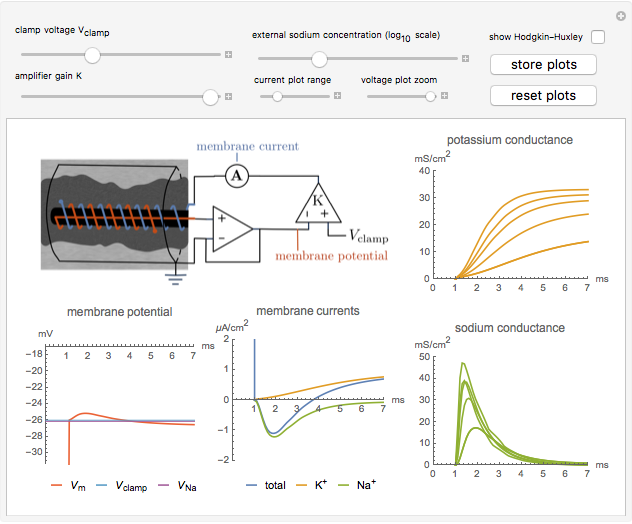
Snapshot 2: the dependence of the conductances on the magnitude of the voltage step and gain of the clamp circuit can be explored

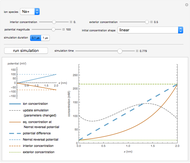
Snapshot 3: the Hodgkin–Huxley model of the ionic conductances can be shown to validate the theory

The Hodgkin–Huxley neuron model is a seminal discovery in neuroscience and electrophysiology. It describes the ionic currents and resulting voltage changes that occur across a neuron's membrane. Practically, it was developed by measuring the membrane conductance of sodium and potassium ions in the giant axon of the squid Loligo, from which the governing differential equations are deduced. The essential procedure of the original experiment [1, 2] is described below.

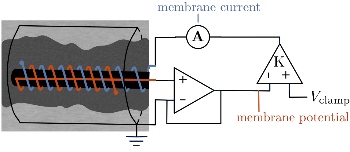
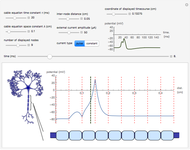
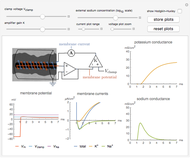
1. A voltage and current electrode, wrapped in a glass capillary, are inserted in the giant axon (0.1 to 1 mm diameter) as shown in the diagram. The axon itself is held in place in a grounded cylinder, originally made of silver sheet. The potential across the membrane is stepped and held at a constant value using a voltage clamp [1].

The high impedance op-amp draws minimal current from the membrane, and roughly outputs the membrane voltage 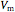. The amplifier has an adjustable gain 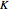, and outputs voltage 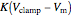. The resultant current is applied across the membrane using the current electrode, leading to a feedback circuit that at high gain fixes the membrane voltage 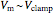[3].

When the potential across the membrane is constant, the sum of the ionic currents must be balanced by the current applied by the voltage clamp. Thus, the measured current applied by the clamp 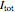is the same magnitude as the total ionic current across the membrane (and opposite in sign). The total ionic current is divided into three components: 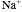, , 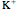and leak (other ions).

2. Next, in a separate experiment, the components of the total current are determined. The extracellular sodium concentration is adjusted such that sodium current does not occur [2], given by

,

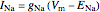where 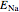is the Nernst reversal potential. Clearly, at .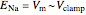

The reversal potential is given by

,

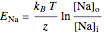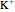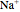where and denote the variable extracellular and fixed intracellular concentrations, is the charge of and , and 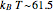at 37° C [3].

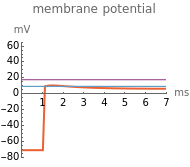
When 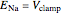, as can be seen in the lower-left panel, the sodium current disappears. Since the leak and capacitive currents occur on a short timescale much less than 1 ms (seen in the blue spike at 1 ms in the bottom-middle panel), principally only the potassium current remains. The measured total current is now 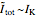, shown in orange. The sodium current is obtained as 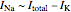, with from step 1, shown in green.

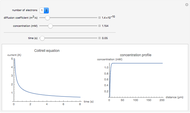
3. Once the ionic currents have been determined, the conductances are given by

,

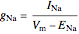and similarly for 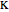[3].

The time-dependent behavior of the conductances is explained by the transitions of activation and inactivation particles ,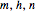

,

,

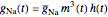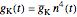where the particle dynamics are described by

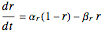
for 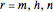, and where , 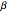are transition rates between open and closed states. For further information, see [3, 4].

The true conductances may be shown on the plots for validation of the theory. Combined with the dynamics of the membrane voltage,

;

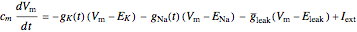these equations constitute the Hodgkin–Huxley model [3, 4].

References

[1] A. L. Hodgkin, A. F. Huxley, and B. Katz, "Measurement of Current-Voltage Relations in the Membrane of the Giant Axon of Loligo," The Journal of Physiology, 116(4), 1952 pp. 424–448. doi:10.1113/jphysiol.1952.sp004716.

[2] A. L. Hodgkin and A. F. Huxley, "Currents Carried by Sodium and Potassium Ions through the Membrane of the Giant Axon of Loligo," The Journal of Physiology, 116(4), 1952 pp. 449-472. doi:10.1113/jphysiol.1952.sp004717.

[3] C. Koch, Biophysics of Computation: Information Processing in Single Neurons, New York: Oxford University Press, 1999.

[4] A. L. Hodgkin and A. F. Huxley, "A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve," The Journal of Physiology, 117(4), 1952 pp. 500–544. doi:10.1113/jphysiol.1952.sp004764.