The Malfatti Problem

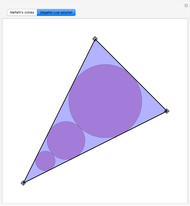
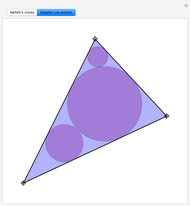
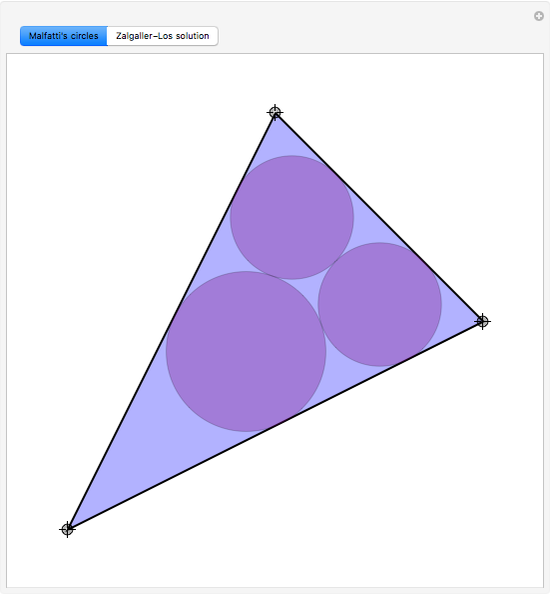
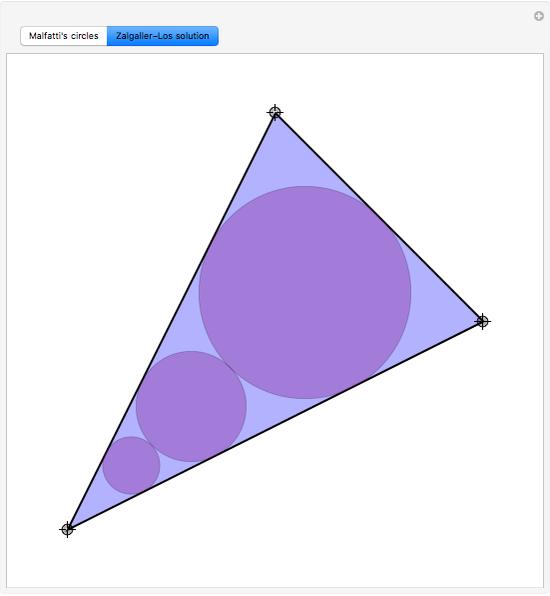
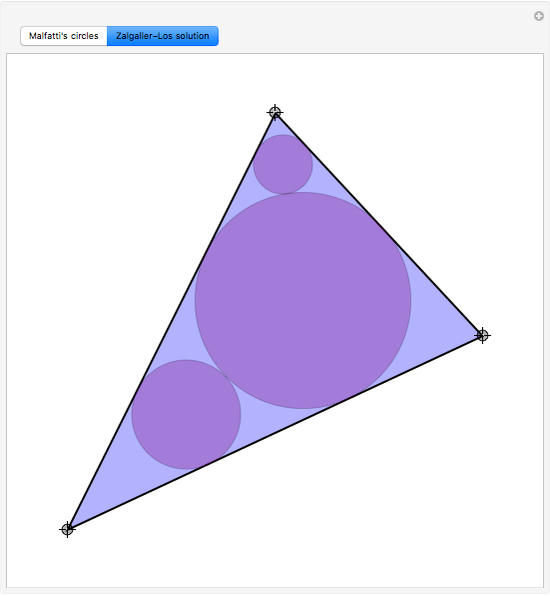
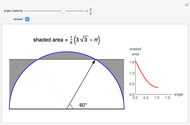
In 1803 Malfatti proposed the following problem: given an arbitrary triangle, find three non-intersecting circles inside it so that the sum of the areas is maximized. He wrongly assumed that it was equivalent to the problem of finding three circles (since then known as Malfatti circles) each of which is tangent to the other two and to two sides of the triangle. Actually, the problem of obtaining Malfatti circles was formulated and solved by Chokuyen Ajima (1732–1798) as a purely geometric problem. It was not until 1929 that Lob and Richmond noted that the Malfatti circles were not always the solution to the Malfatti problem. In 1967, Goldberg proved that the Malfatti circles in fact never solve the Malfatti problem! Malfatti's problem was solved by Zalgaller and Los only in 1991. This Demonstration shows the Malfatti circles and the Zalgaller–Los solution, which always includes the incircle of the triangle.