Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

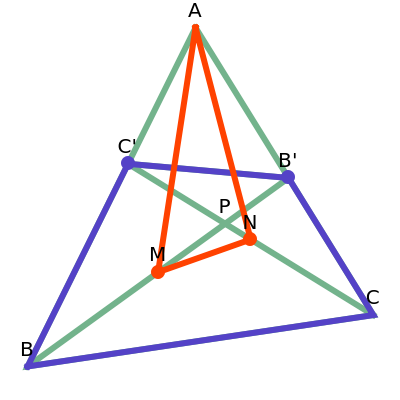
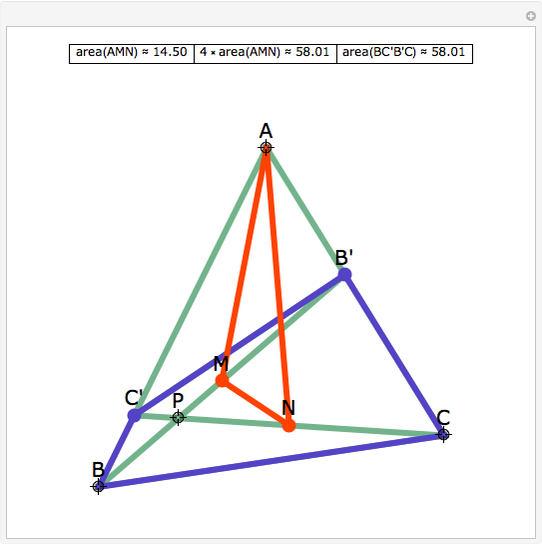
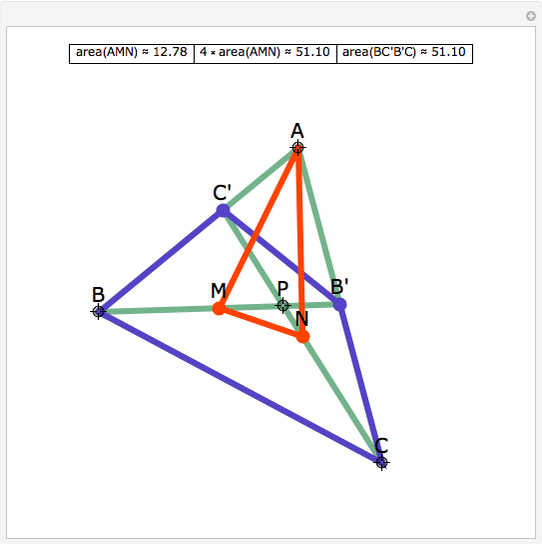
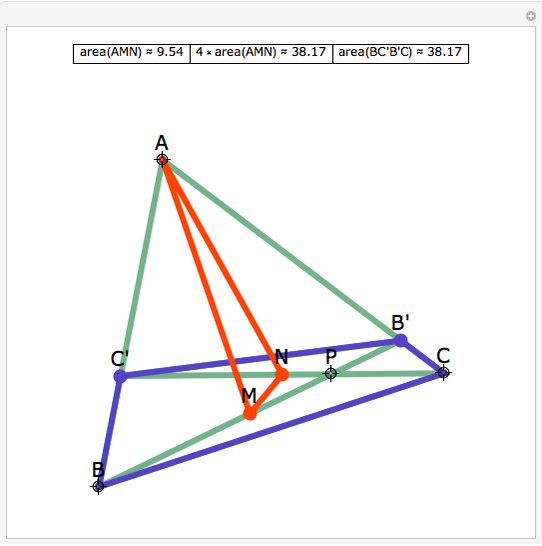
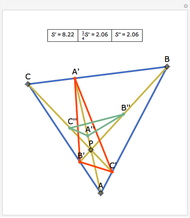
The Midpoints of Two Cevians

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

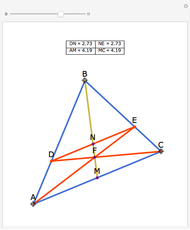
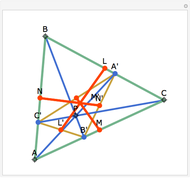
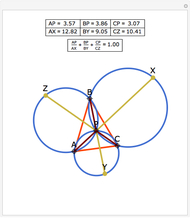
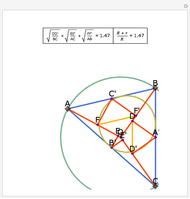
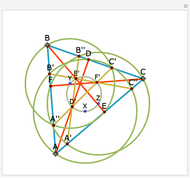
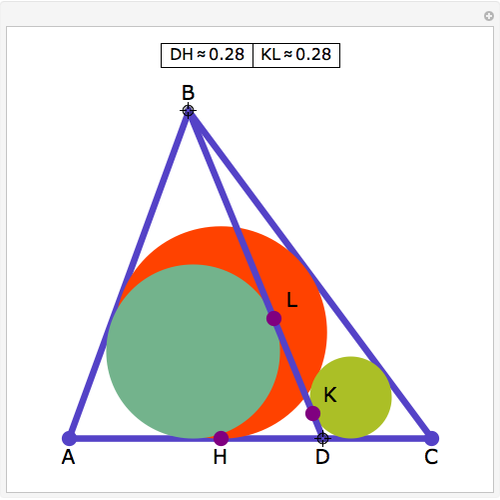
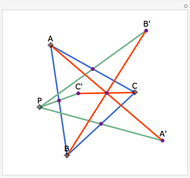
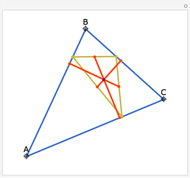
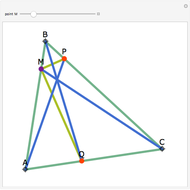
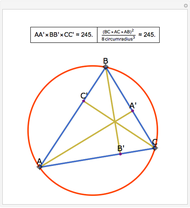
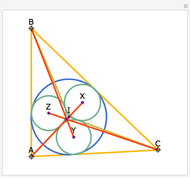
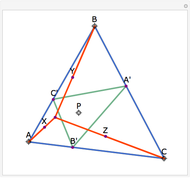
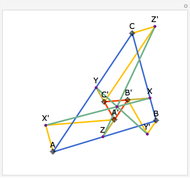
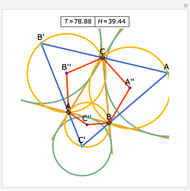
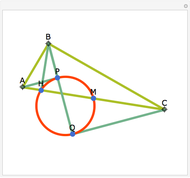
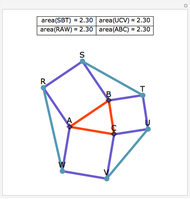
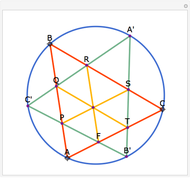
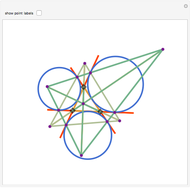
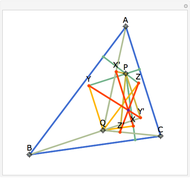
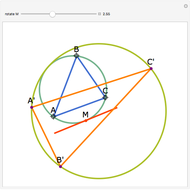
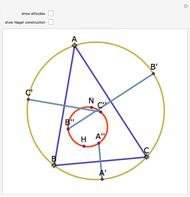
A cevian is a line drawn from a vertex of a triangle to the opposite side.

[more]

Let ABC be a triangle and let M and N be the midpoints of the cevians BB' and CC'. Then the area of the quadrilateral BC'B'C is 4 times the area of AMN.

[less]

Contributed by: Jay Warendorff (March 2011)
After work by: Antonio Gutierrez
Open content licensed under CC BY-NC-SA

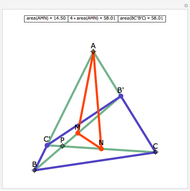
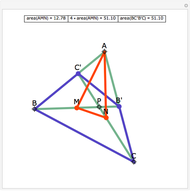
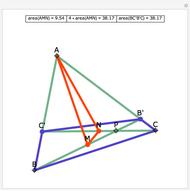
Snapshots

Details

The statement of the theorem is in Problem 90. Quadrilateral and Triangle Areas, Midpoints.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send