The Misdirection Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
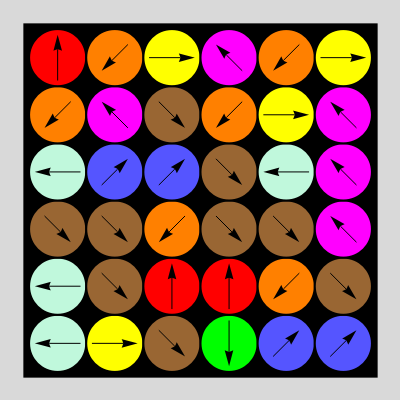
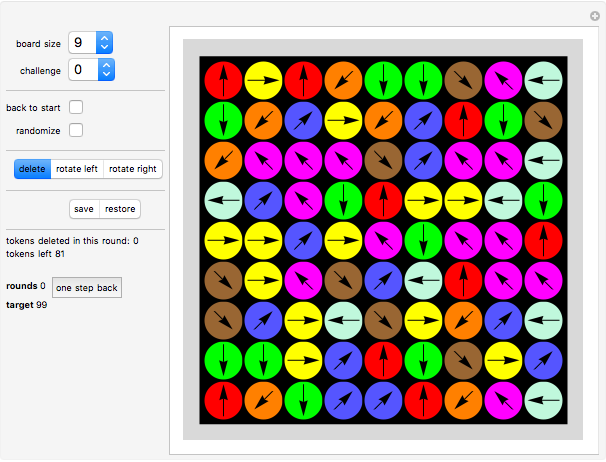
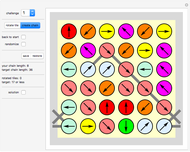
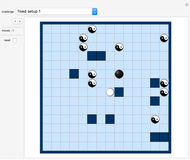
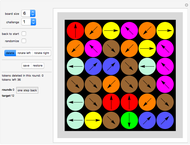
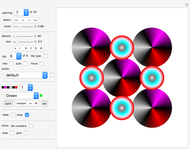
In the "Misdirection" game you try to delete all tokens from the wraparound board in as few moves as possible. There are three types of moves: delete, rotate left and rotate right. Decide which type of move you would like to make, then click a disk.
Contributed by: Karl Scherer (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Goal
You get the message "YOU WON" if you clear the board using no more moves than the target.
Moves
If you choose "delete" for a move, then the token on this clicked position will be deleted. The arrow that was shown on the deleted token pointed in one of eight directions. A token lying in the direction of the arrow will also be deleted and so on, until you land on a position that has no appropriate neighbor.
If you choose "rotate left" or "rotate right", a token on the clicked position will rotate counterclockwise or clockwise, by 45° at a time.
Selecting the move mode does not count as a move.
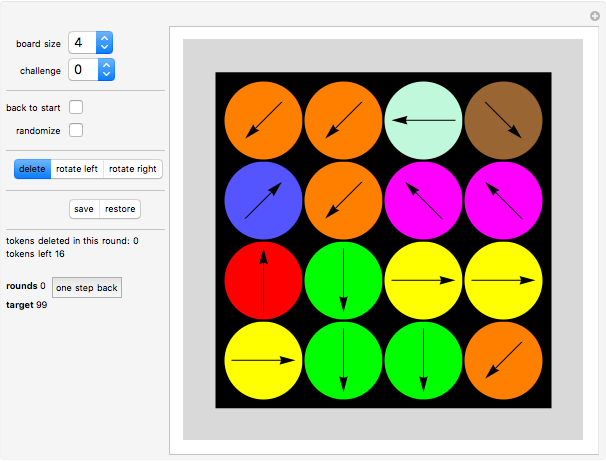
Controls
Click "board size" to choose a board of size 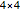 ,
, 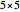 ,
, 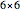 ,
, 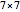 ,
, 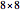 or
or 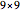 .
.
For board size 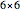 , the "challenge" button shows 10 setups to choose from.
, the "challenge" button shows 10 setups to choose from.
Click the "back to start" button to return to the starting position.
Click the "randomize" button to change the arrow directions in the current setup.
Use the "save" or "restore" buttons to save and restore a board setup you want to keep.
Move modes: you can choose among "delete" mode, "rotate left" mode and "rotate right" mode. "Rotate left" rotates a compass counterclockwise; "rotate right" rotates it clockwise.
The "tokens deleted in this round" counter shows the number of tokens deleted.
The "tokens left" counter shows how many tokens remain on the board.
The "rounds" counter counts how many moves have been made.
Click "one step back" to undo the latest move.
The "target" counter shows the length of the shortest known game.
History
"Misdirection" is one of many board games the author has invented; most of them are encoded as Zillions games.
Note
"Misdirection" can also played as a two-player game: player A plays the 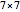 board and writes down how many moves they need, then clicks "back to start". Player B has to solve the same
board and writes down how many moves they need, then clicks "back to start". Player B has to solve the same 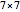 setup. Then both players solve a random
setup. Then both players solve a random 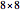 setup, then a
setup, then a 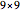 and so on.
and so on.
The players add up the number of moves they each make and the player with the smaller total number of moves wins.
Permanent Citation