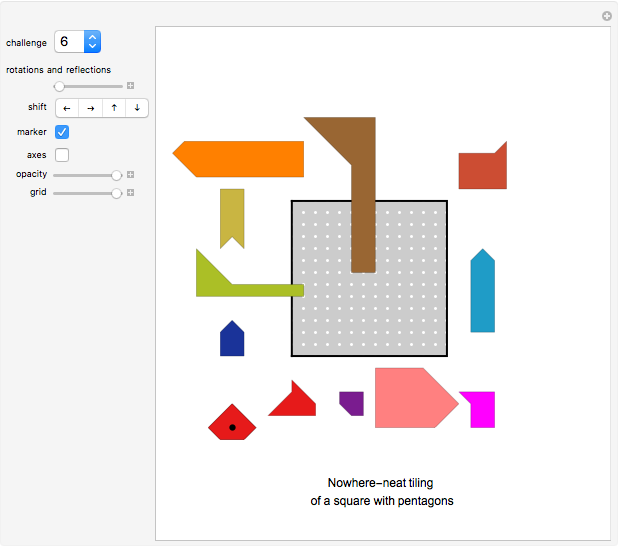
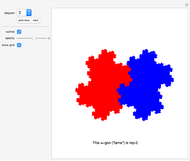
Nowhere-Neat Tilings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
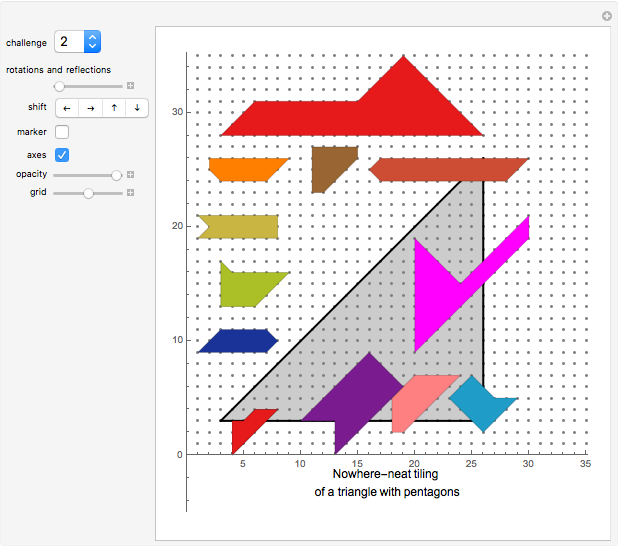
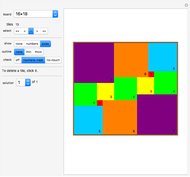
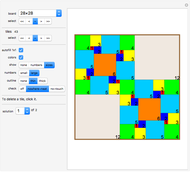
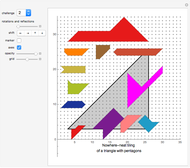
Rearrange the given tiles to create a nowhere-neat tiling of the given gray area.
[more]
Contributed by: Karl Scherer (April 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If no two tiles in a tiling have a full side in common, the tiling is called nowhere-neat, a term introduced by the author of this Demonstration in his 1994 book Nutts and Other Crackers on geometrical problems in the plane, and more deeply researched in his 1999 book New Mosaics.
Controls
You can click and drag the tiles.
The tile clicked last is marked by a black dot.
Click the "marker" switch to make the marker invisible.
The slider bar "rotations and reflections" allows you to rotate and mirror the selected tile.
The setter bar "shift" allows you to shift the selected tile one step into one of four directions.
Click the "axes" option to display the  and
and 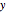 axes.
The option "opacity" makes the tiles transparent.
The option "grid" controls the gray value (between white and black) of the grid colour.
axes.
The option "opacity" makes the tiles transparent.
The option "grid" controls the gray value (between white and black) of the grid colour.
"solution": solutions for challenges 1, 3, 4, 5, and 7 are given.
Mathematical problems of special interest:
The main mathematical problem connected with nowhere-neat tilings is:
(a) to find nowhere-neat tilings of  -gons with
-gons with 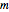 -gons, and
-gons, and
(b) to find all nowhere-neat tilings of the plane using only very few prototiles.
Many interesting results surfaced from research on (a) and (b).
Solutions to part (a):
This Demonstration shows a few examples of part (a).
Related games: the Zillions games "Square the Square", "Square the Square II", "Square the Rectangle".
The main mathematical results for (a) are on tiling a square or rectangle with smaller squares in a nowhere-neat way:
General Theorem on Nowhere-Neat Tilings of Squares with Squares
A square has a nowhere-neat tiling if its sidelength is 11, 16, 18, 19, 20, or greater
than 21. The tiling can always be chosen to contain the unit square 1×1 as a tile.
Additionally, the tiling can be chosen to be fault-free, except for the case 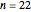 .
.
(By Karl Scherer; proof published in The Journal of Recreational Mathematics, 32(1), 2003–04 pp. 1–13. Patrick Hamlyn solved the cases 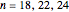 . The proof is also attached to the Zillions games "Square the Square" and "Square the Square II".)
. The proof is also attached to the Zillions games "Square the Square" and "Square the Square II".)
See also the Demonstration "Nowhere-Neat Squaring The Square" by the same author.
In 2005 the author also proved a similar theorem for squaring rectangles:
General Theorem on Nowhere-Neat Tilings of Rectangles with Squares
There is a nowhere-neat tiling as long as the rectangle is sufficiently large. To be precise, there is a fault-free nowhere-neat tiling for each 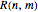 with
with  and
and 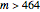 . Additionally, each such solution can be chosen to contain the 1×1 square and hence is not an enlargement of a smaller tiling.
. Additionally, each such solution can be chosen to contain the 1×1 square and hence is not an enlargement of a smaller tiling.
(Karl Scherer, proof attached to his Zillions game "Square the Rectangle".)
Similar theorems (by the same author) hold for no-touch tilings.
It is the author's conjecture that all rectangles and squares of size 22×22 or larger have a fault-free nowhere-neat tiling that is not an enlargement of a smaller tiling. This conjecture is based on the fact that all rectangles of size 22×22 up to 50x50 have such a tiling.
Solutions to part (b):
See Demonstrations "Nowhere-Neat Tilings Of The Plane" and "Nowhere-Neat Tilings Of The Plane, Part 2" .
Permanent Citation