The Prisoner's Dilemma

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
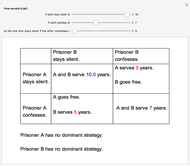
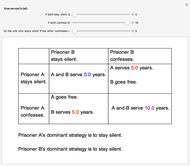
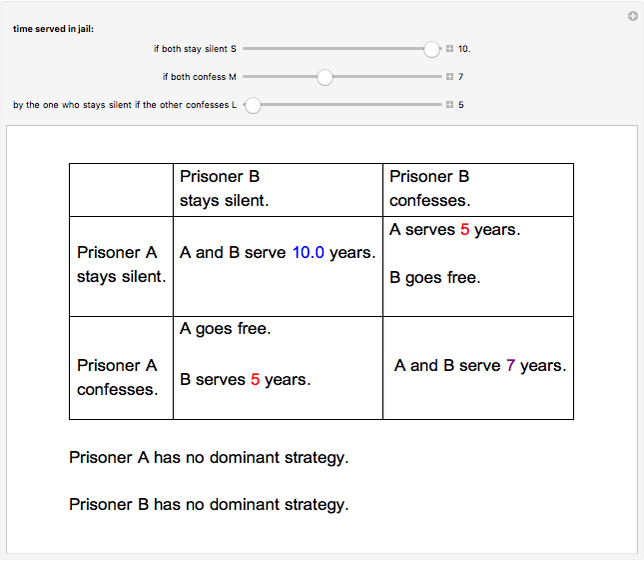
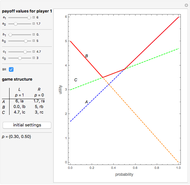
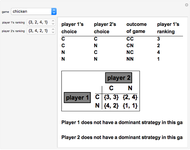
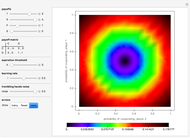
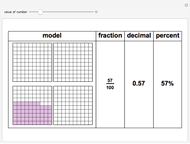
Two suspects, A and B, are taken into custody by the police. The police do not have sufficient evidence for a conviction so they separate the prisoners and visit them individually to offer them the same deal. If one confesses and will testify against the other while the other still stays silent, the one who testifies will go free while the other will serve a very long time  in jail. However, if both confess, then both will spend a medium time
in jail. However, if both confess, then both will spend a medium time  in jail. Finally, if both stay silent they will serve a very short period of time
in jail. Finally, if both stay silent they will serve a very short period of time  in jail.
in jail.
Contributed by: Sarah Lichtblau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
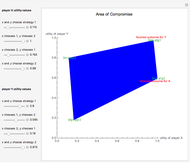
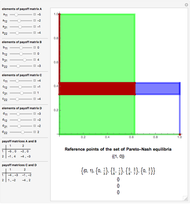
An outcome of a game is Pareto optimal if no other outcome makes every player at least as well off and at least one player better off.
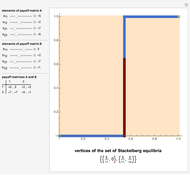
A dominant strategy occurs when one strategy is better than any other for one player regardless of the other players' actions.
Permanent Citation