Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Third Pedal Triangle of a Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

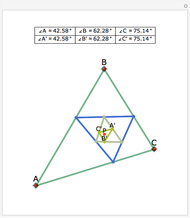
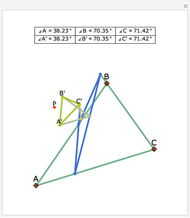
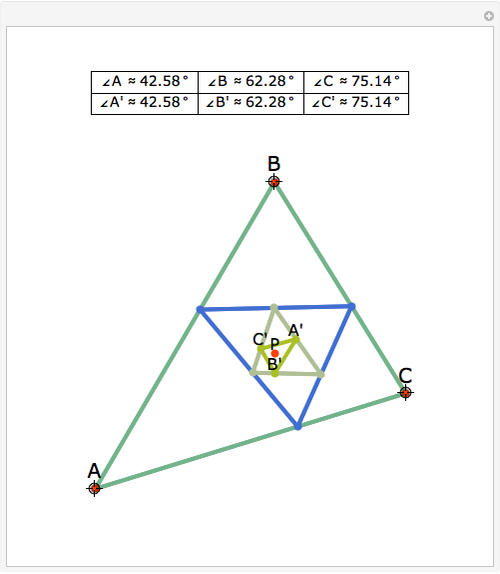
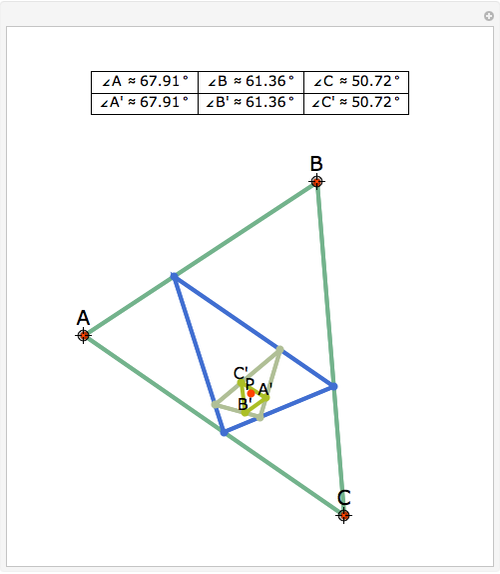
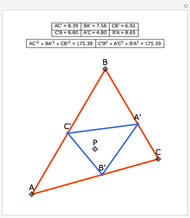
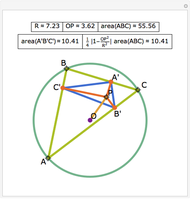
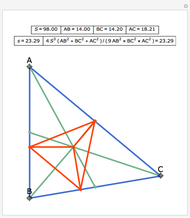
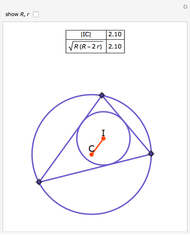
The triangle formed by projecting a point onto the sides of a triangle is a pedal triangle.

[more]

The pedal triangle of a point with respect to the pedal triangle with respect to the pedal triangle with respect to the triangle is similar to the triangle.

Drag the red points to change the figure.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information, see Pedal Triangles.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send