Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Angle Bisectors in a Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

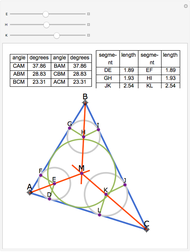
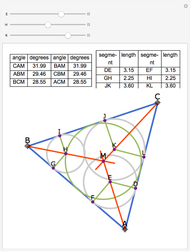
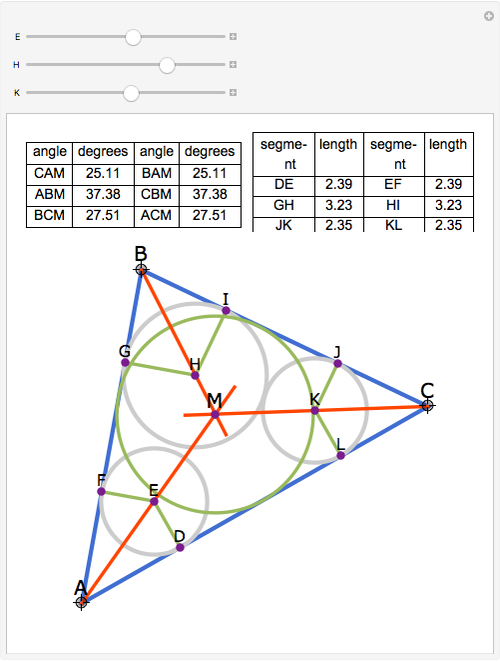
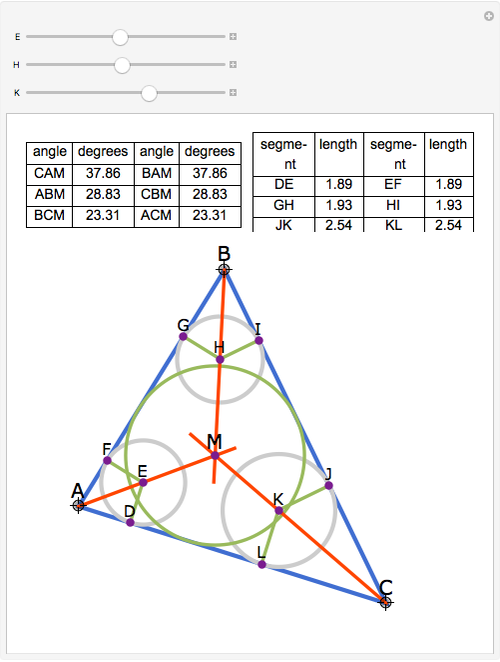
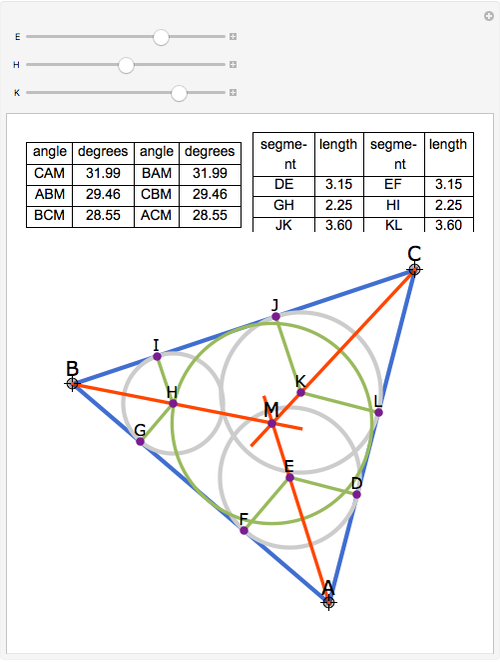
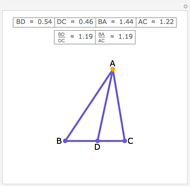
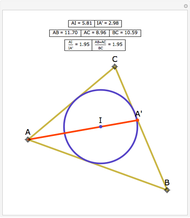
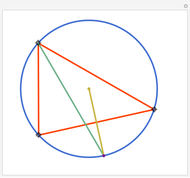
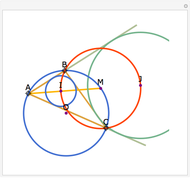
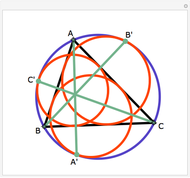
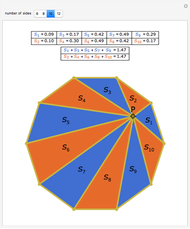
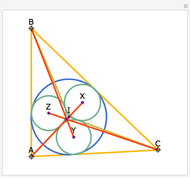
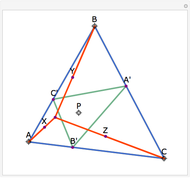
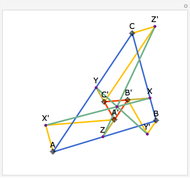
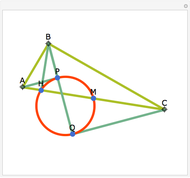
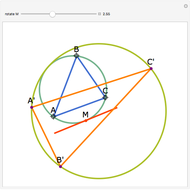
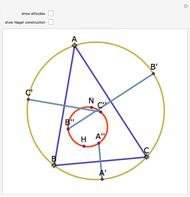
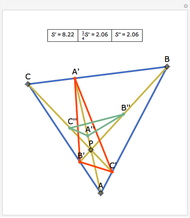
The angle bisectors of a triangle ABC meet in a single point called the incenter. The incenter M is equidistant from the three sides of the triangle. The incenter is the center of the incircle, the largest circle inside ABC. The incircle is tangent to all three sides.

[more]

You can change the locations of E, H, and K on the angle bisectors.

If DE and EF are the perpendiculars from E to AC and AB, then |DE| = |EF|. Similarly, |GH| = |HI| and |JK| = |KL|.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information visit Anatomy of Triangles.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send