The Troublesome Twelve Circle Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
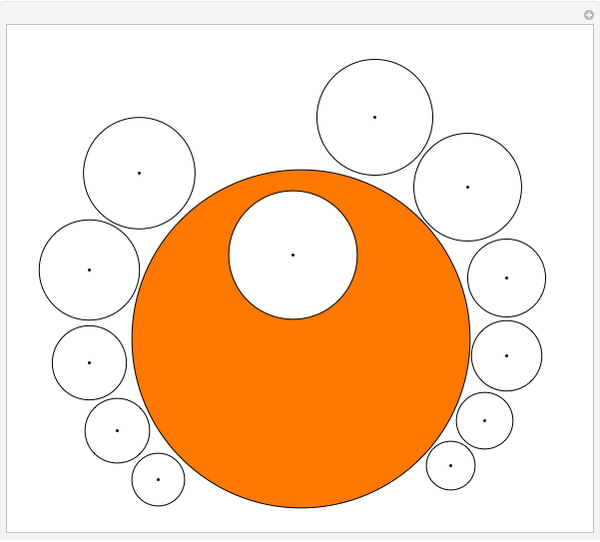
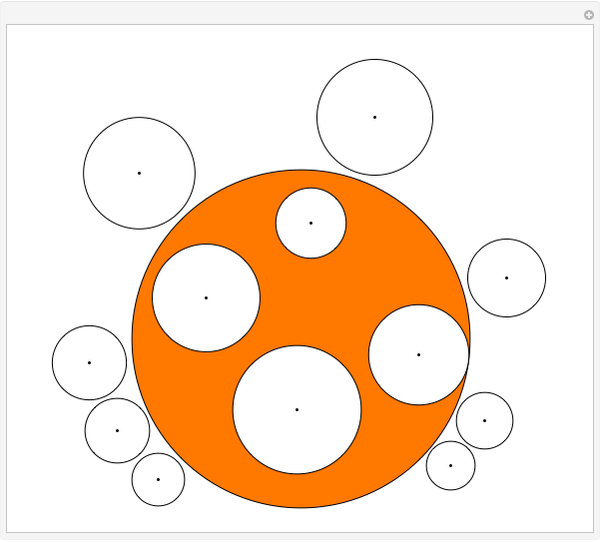
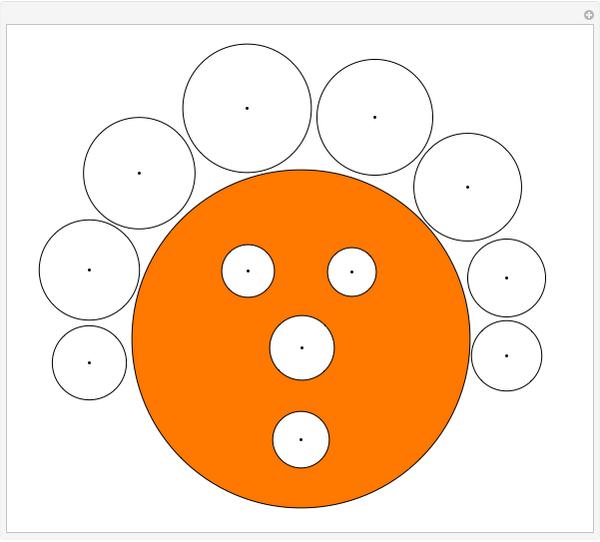
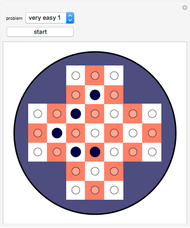
Move all the white disks onto the orange disk so that none of the white disks overlap. This puzzle, named Twubblesome Twelve, has several unintended solutions.
Contributed by: Bill Gosper (March 2011)
Based on a program by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the last several years I've sought to make challenging puzzles based on packing a given set of disks into a given cavity. Unique solutions are nicer and presumably harder to find, so no two disks should be close in size. On the other hand, if the sizes are widely disparate, the smallest disks fit between the largest, and are simply redundant. These conflicting criteria become nearly impossible to meet as the number of disks reaches twelve, where the sheer number of configurations also works against uniqueness. To make matters worse, it appears to be infeasible to check for uniqueness computationally, or even solve these puzzles at all without simplifying assumptions.
For circular cavities, the best I have done is eleven disks (The Huddle), with various attempts at twelve (Twubblesome Twelve (shown here), TTII, ...) cooked by expert solvers. Perversely, the unintended solutions have generally been looser than the apparently close-packed "mathematical" solutions, which probably could be found by a sufficiently clever program.
Noncircular cavities enormously complicate things for both the designer and the solver. For example, the designer no longer has a family of cavity-preserving Moebius transformations on the disk sizes, and the solver (e.g., a program) is faced with a continuum of distinguishable places to start. And by precluding rotations and reflections, an asymmetrical cavity cuts the solution space by another factor of four. Perhaps best of all, given the size constraints on the disks, it seems possible to fill a slightly greater percentage of a noncircular cavity, although the computations are formidable. Greater coverage leaves fewer solutions.
Experts again cooked my early attempts (Octave, Arnold Laidanegger, ...). For my current best design, named Arnold Dozenegger, I spent months repeatedly solving systems of 33 polynomials, many with 3367 terms and 36 unknowns. It very probably falls short of optimal coverage, but so far, no one has found even the intended solution, let alone a bogosity (excepting early prototypes that were cut too loose, plus one violent cramming that distorted the cavity).
Permanent Citation
"The Troublesome Twelve Circle Problem"
http://demonstrations.wolfram.com/TheTroublesomeTwelveCircleProblem/
Wolfram Demonstrations Project
Published: March 7 2011