Water-Pouring Problem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
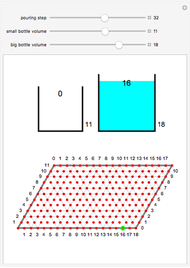
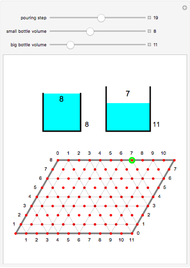
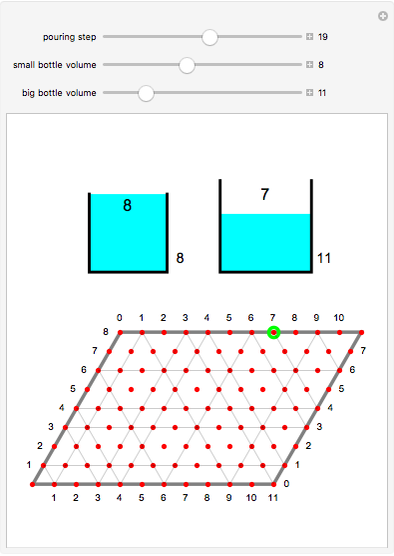
A classic puzzle starts with two unmarked bottles that can hold 3 liters and 5 liters respectively, and a bathtub with unlimited water. How can 1 liter be measured?
[more]
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Water-Pouring Problem"
http://demonstrations.wolfram.com/WaterPouringProblem/
Wolfram Demonstrations Project
Published: March 7 2011