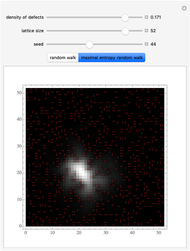
The "True" Self-Avoiding Random Walk in Z

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
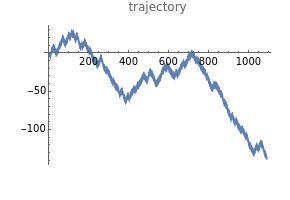
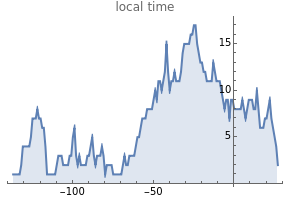
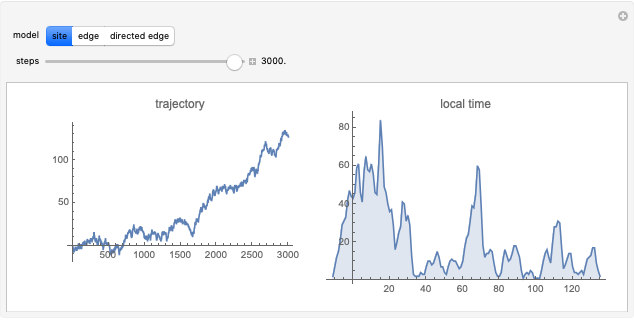
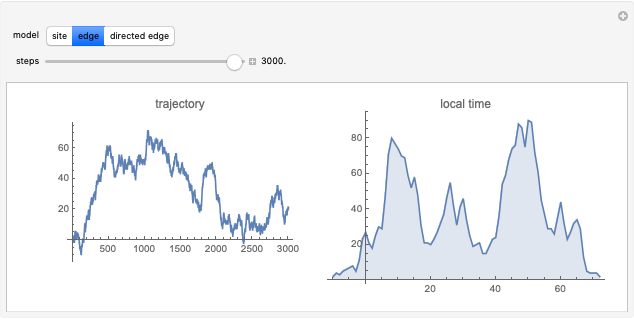
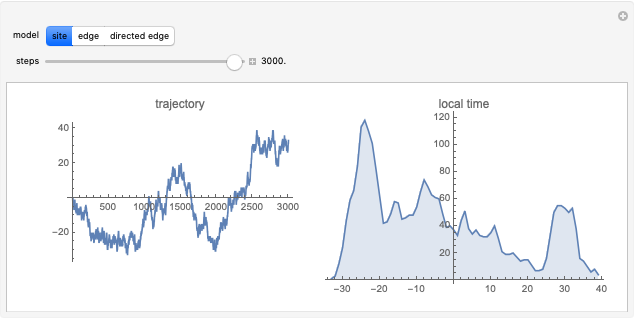
The "true" self-avoiding walk is a natural example of non-Markovian random walks. In these one-dimensional nearest neighbor models, the walker is self-repellent, that is, it is pushed by the negative gradient of its own local time. More informally, the walker prefers places that it has visited fewer times in the past. The site repulsion and edge repulsion models behave similarly; the displacement scales with time to the power 2/3, and the limit is a complicated, but well-defined object, with the local time picture converging to a system of reflected and absorbed Brownian motion. In the directed edge repulsion model, the proper scaling is diffusive, but there is no continuous limit process, and the trajectories are much rougher. The graph of the local times converges to a deterministic triangular shape.
Contributed by: Balint Veto, Budapest University of Technology and Economics (BME), Department of Stochastics (March 2011)
Additional contributions by: János Tóth
Open content licensed under CC BY-NC-SA
Snapshots
Details
In tree models, local time is defined differently. In the site repulsion case, we denote by  the number of visits to site
the number of visits to site 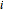 until time
until time  , and call that local time. Then the transition probabilities are proportional to the negative exponential of the local time differences, that is,
, and call that local time. Then the transition probabilities are proportional to the negative exponential of the local time differences, that is,  and
and 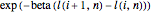 are, after normalization, the probabilities of
are, after normalization, the probabilities of 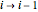 and
and 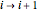 jumps. (In the simulation,
jumps. (In the simulation, 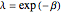 .) This model was introduced in the following paper, but the problem is still open.
.) This model was introduced in the following paper, but the problem is still open.
D. Amit, G. Parisi, and L. Peliti, "Asymptotic Behaviour of the "True" Self-Avoiding Walk," Phys. Rev. B, 27, 1983 pp. 1635–1645.
A continuous time version of the site repulsion model is solved in
B. Tóth and B. Vető, "Continuous Time "True" Self-Avoiding Random Walk on Z," arXiv, 2009.
The edge repulsion model is believed to have similar limit behavior. Here, the local time  is the number of crossings through the edge
is the number of crossings through the edge  up to time
up to time  . The transition probabilities are proportional to
. The transition probabilities are proportional to 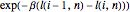 and
and 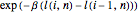 . The scaling limit of the random walk is the "true" self-repelling motion after scaling with time to the 2/3 power. In this limit, the sequence of local times converges in distribution to a system of reflected and absorbed Brownian motions, which appears in the construction of the Brownian web. The limit theorems for the edge repulsive random walk and the construction of the "true" self-repelling motion can be found in
. The scaling limit of the random walk is the "true" self-repelling motion after scaling with time to the 2/3 power. In this limit, the sequence of local times converges in distribution to a system of reflected and absorbed Brownian motions, which appears in the construction of the Brownian web. The limit theorems for the edge repulsive random walk and the construction of the "true" self-repelling motion can be found in
B. Tóth, "The 'True' Self-Avoiding Walk with Bond Repulsion on Z: Limit Theorems," Ann. Probab., 23, 1995 pp. 1523–1556.
B. Tóth and W. Werner, "The True Self-Repelling Motion," Probab. Theory Relat. Fields, 111, 1998 pp. 375–452.
In the directed edge repulsion model, the local times 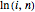 and
and 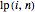 are defined by the number of uses of the directed edges
are defined by the number of uses of the directed edges  and
and  , respectively, until time
, respectively, until time  . (In this notation,
. (In this notation,  stands for negative direction, and
stands for negative direction, and 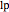 for positive direction.) The transition probabilities are proportional to
for positive direction.) The transition probabilities are proportional to 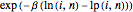 and
and 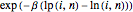 . Surprisingly, with these settings, the limit behavior of the random walk is diffusive. After scaling the time by the square root, the one-dimensional marginal is uniformly distributed, but there is no continuous limit process. The sequence of local times converges to a deterministic triangular limit shape. See
. Surprisingly, with these settings, the limit behavior of the random walk is diffusive. After scaling the time by the square root, the one-dimensional marginal is uniformly distributed, but there is no continuous limit process. The sequence of local times converges to a deterministic triangular limit shape. See
B. Tóth and B. Vető, "Self-Repelling Random Walk with Directed Edges on Z," Electronic Journal of Probability, 13, 2008 pp. 1909–1926.
The author of this Demonstration thanks János Tóth for his help in preparing this work in Mathematica.
Permanent Citation