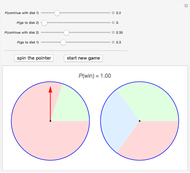
A Reluctant Random Walk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
There are  cards labeled 1, 2, ...,
cards labeled 1, 2, ...,  . Initially, the cards are randomly divided between two players, A and B. For example, if
. Initially, the cards are randomly divided between two players, A and B. For example, if  is even, each player could get half of the cards. At each move of the game, one of the numbers from 1 to
is even, each player could get half of the cards. At each move of the game, one of the numbers from 1 to  is chosen at random and the player with this card must give it to the other player. The game continues until one of the player has all the cards. This Demonstration shows games for one of the players, with expected duration and probability of ruin.
is chosen at random and the player with this card must give it to the other player. The game continues until one of the player has all the cards. This Demonstration shows games for one of the players, with expected duration and probability of ruin.
Contributed by: Heikki Ruskeepää (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
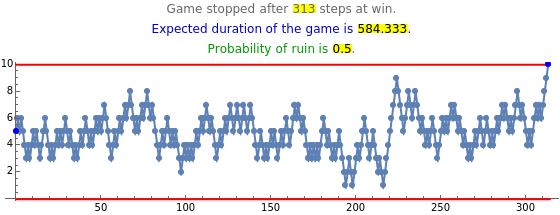
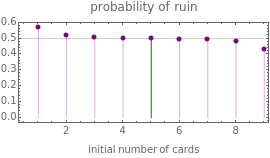
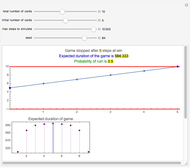
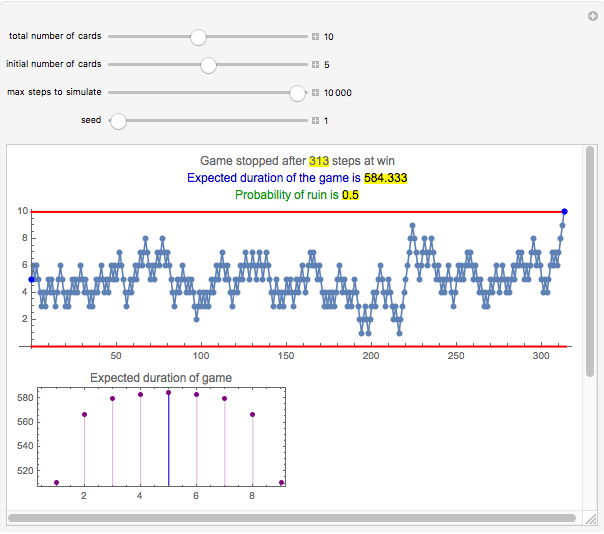
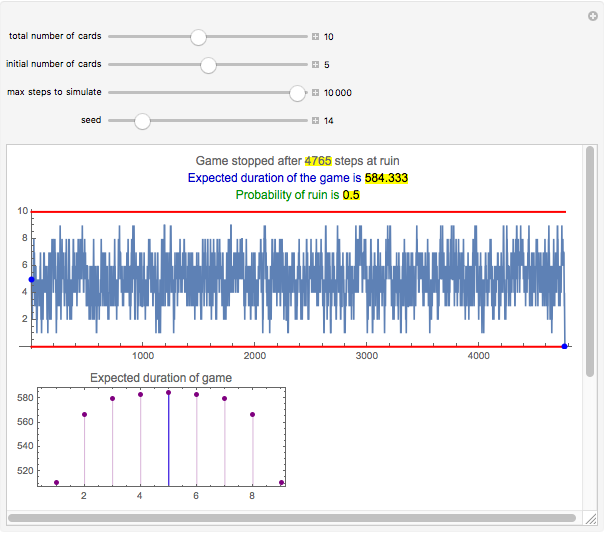
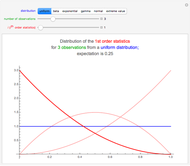
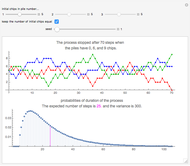
Snapshot 1: There are 10 cards and initially player A has five cards. The game lasted 313 steps and player A won the game. In this example, the expected duration is approximately 584 steps. The lower-left plot shows that the duration does not depend much on the initial number of cards; this is the result of the random walk having the tendency to move away from the absorbing barriers. Even with one or nine cards, the expected duration is only somewhat smaller, 511. Similarly, the probability of ruin does not depend much on the initial number of cards and is quite near to 0.5 for all initial numbers of cards. Only the case of having initially one or nine cards has a somewhat larger effect to the probability of ruin.
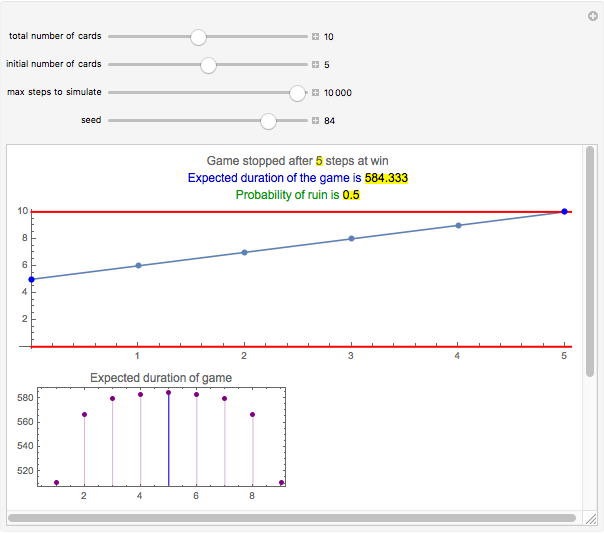
Snapshot 2: The initial situation is as in the first snapshot. However, now the game lasted the minimum number of steps, five.
Snapshot 3: Again this starts as in snapshot 1, but the game lasted 4765 steps!
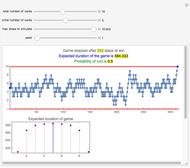
Snapshot 4: With only six cards, the expected duration of the game is 37.
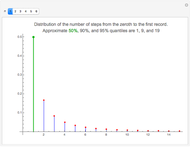
Snapshot 5: With 20 cards, the expected duration of the game is over a half-million steps!
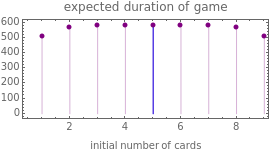
Here are the expected durations of the game (rounded to the nearest integer) for 2, 4, 6, …, 20 cards where player A initially has half of the cards:
2: 1
4: 8
6: 37
8: 149
10: 584
12: 2283
14: 8965
16: 35367
18: 140019
20: 555691
The discrete-time Markov chain is as follows. The walker A moves among the points 0, 1, 2, …,  . The chain is said to be currently in state
. The chain is said to be currently in state 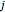 if player A has
if player A has 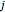 cards. The walker moves from state
cards. The walker moves from state 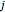 to state
to state  with probability
with probability 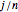 and to state
and to state 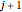 with probability
with probability 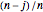 . States 0 and
. States 0 and  are absorbing, so that the chain remains in state 0 or
are absorbing, so that the chain remains in state 0 or  once it is achieved. For example, the walker moves from state 1 to state 0 or from state
once it is achieved. For example, the walker moves from state 1 to state 0 or from state  to state
to state  only with probability
only with probability 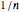 . This implies that the walker hesitates to stop.
. This implies that the walker hesitates to stop.
Consider the expected duration of the game. Let 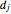 be the expected duration if player A initially has
be the expected duration if player A initially has 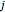 cards. After the first step, A has either
cards. After the first step, A has either  cards with probability
cards with probability  or
or 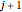 cards with probability
cards with probability 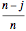 . Thus, by the theorem of total expectation,
. Thus, by the theorem of total expectation, 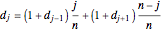 . This recurrence equation can be solved for
. This recurrence equation can be solved for 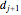 in terms of
in terms of 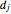 and
and 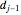 . Clearly, the initial condition is
. Clearly, the initial condition is 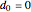 . It can be shown [1] that
. It can be shown [1] that 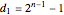 .
.
Consider then the probability of ruin. Let 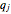 be the probability of ruin if player A initially has
be the probability of ruin if player A initially has 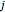 cards. By the theorem of total probability,
cards. By the theorem of total probability, 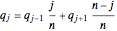 . This equation can be solved for
. This equation can be solved for 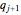 in terms of
in terms of 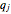 and
and 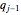 . As to initial conditions, clearly
. As to initial conditions, clearly 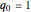 . It can be shown [1] that
. It can be shown [1] that 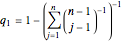 .
.
The reluctant random walk can be compared with the so-called gambler's ruin process; see The Gambler's Ruin. Assume, for example, that player A initially has five dollars and that the casino also has five dollars. At each step, player A wins or loses one dollar with probability 0.5. The game stops once A has 0 or 10 dollars. The expected duration of this game is only 25. Recall that in the reluctant random walk the corresponding expected duration was 584.
This Demonstration is based on [1, pp. 34–37].
[1] J. Andel, Mathematics of Chance, New York: Wiley, 2001.
Permanent Citation