Properties of a Simple Random Walk with Boundaries

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
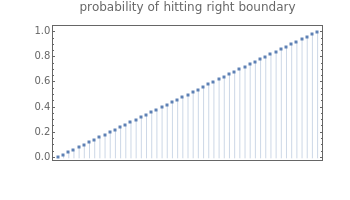
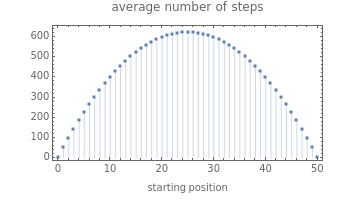
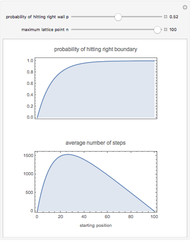
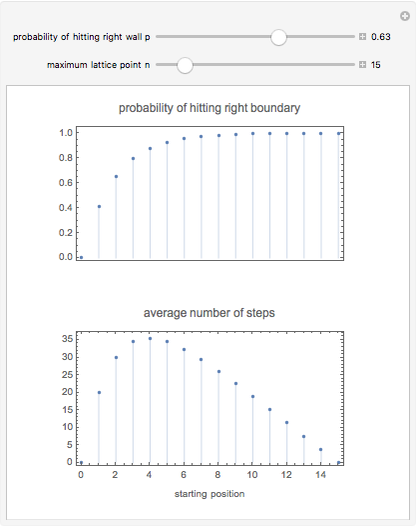
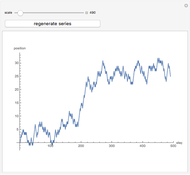
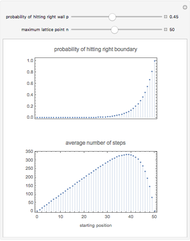
This Demonstration shows several basic properties of random walks on a one-dimensional lattice of points  . At each step, the probability of moving to the right or left is
. At each step, the probability of moving to the right or left is  and
and  , respectively; the walk ends when it reaches
, respectively; the walk ends when it reaches  or
or  . As a function of the starting position
. As a function of the starting position  , we show the probability of the walk ending at the right boundary, and the average number of steps taken during the walk (regardless of which boundary it eventually hits).
, we show the probability of the walk ending at the right boundary, and the average number of steps taken during the walk (regardless of which boundary it eventually hits).
Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA
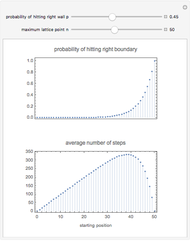
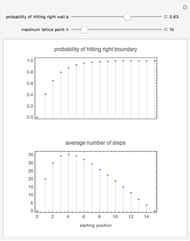
Snapshots
Details
The formulas for these quantities can be found by solving second-order difference equations.
G. Grimmett and D. Stirzaker, Probability and Random Processes, 3rd ed., Oxford: Oxford University Press, 2001.
Permanent Citation
"Properties of a Simple Random Walk with Boundaries"
http://demonstrations.wolfram.com/PropertiesOfASimpleRandomWalkWithBoundaries/
Wolfram Demonstrations Project
Published: March 7 2011