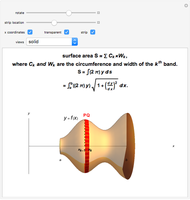
Soap Film between Two Equal and Parallel Rings

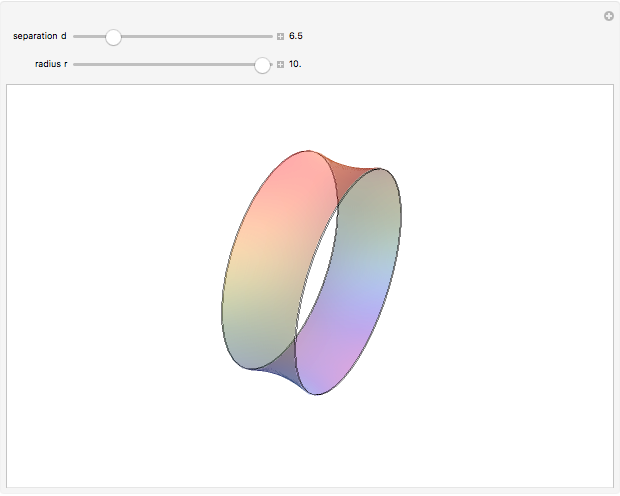
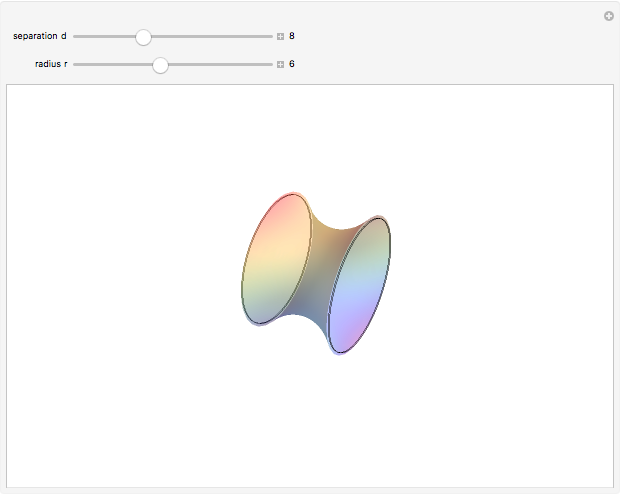
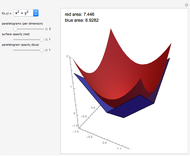
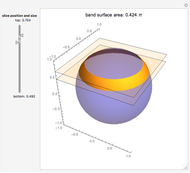
A soap film is formed between two parallel rings of radius separated by a distance . To minimize the surface-tension energy of the soap film, its total area seeks a minimum value. The derivation of the shape of the film involves a problem in the calculus of variations. Let represent the functional form of the film in cylindrical coordinates. The area is then given by . The integrand is determined by the Euler–Lagrange equation 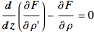, which can be reduced to its first integral 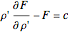, a constant. The solution works out to , a catenary of revolution, with the boundary condition . 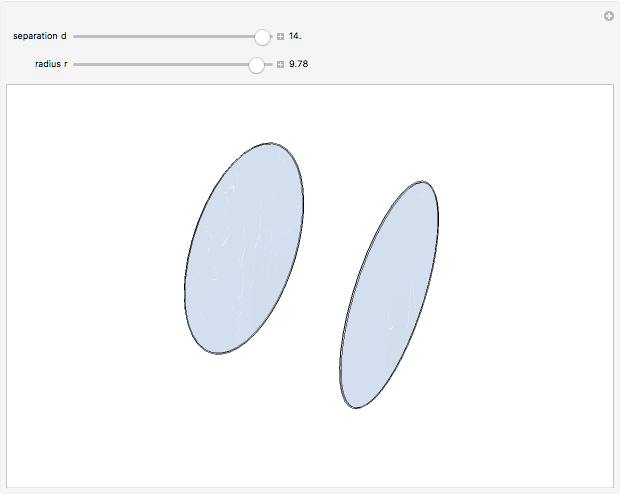When 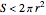, the film collapses to disks within the two rings.