Traveling Salesman Art

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
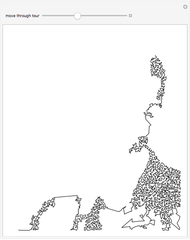
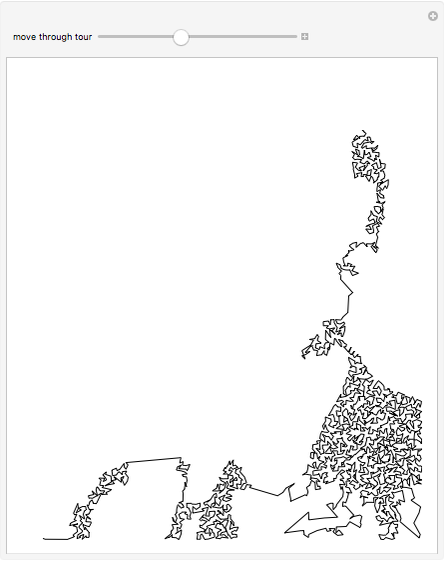
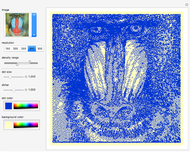
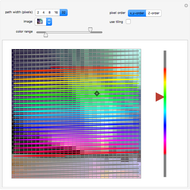
In a picture, random points are selected proportionally to the gray levels of the picture. An algorithm for the "traveling salesman problem"—which asks for the shortest path through a set of cities without passing through any of them twice—is then used to draw a precomputed continuous line with no overlaps through the set of points. This Demonstration lets you see how the tour progresses.
Contributed by: Enrique Zeleny (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The built-in Mathematica command used to calculate the path is 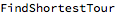 , with the Method option set to "RemoveCrossings".
, with the Method option set to "RemoveCrossings".
The man in the picture is Alan Turing, founder of computer science, born in 1912.
Reference
[1] C. S. Kaplan and R. Bosch. "TSP Art." (May 19, 2005) www.cgl.uwaterloo.ca/~csk/papers/kaplan_bridges2005b.pdf.
Permanent Citation
"Traveling Salesman Art"
http://demonstrations.wolfram.com/TravelingSalesmanArt/
Wolfram Demonstrations Project
Published: June 7 2012