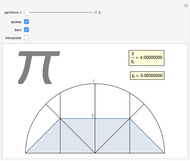
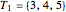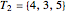Twin and Nearly Twin Pythagorean Triples

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
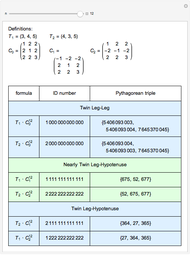
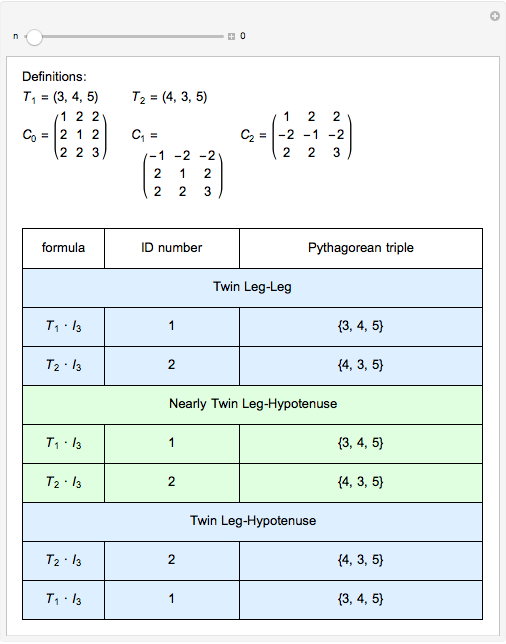
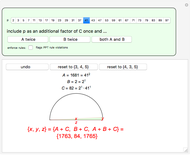
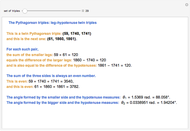
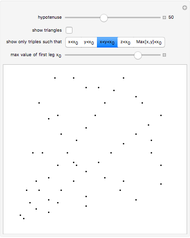
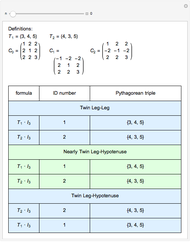
A Pythagorean triple 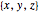 is an ordered set of three positive integers that are the side lengths of a Pythagorean triangle, so that
is an ordered set of three positive integers that are the side lengths of a Pythagorean triangle, so that 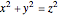 . A twin Pythagorean triple is a Pythagorean triple in which two elements differ by one. In a twin leg-leg Pythagorean triple,
. A twin Pythagorean triple is a Pythagorean triple in which two elements differ by one. In a twin leg-leg Pythagorean triple,  and
and 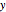 differ by 1; in a twin leg-hypotenuse
differ by 1; in a twin leg-hypotenuse 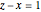 or
or 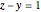 ; in a nearly twin leg-hypotenuse triple,
; in a nearly twin leg-hypotenuse triple, 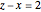 or
or 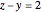 .
.
Contributed by: Robert L. Brown (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
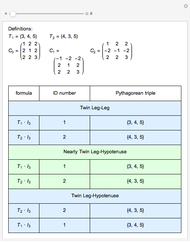
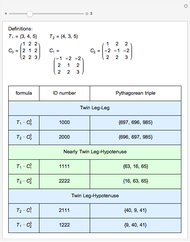
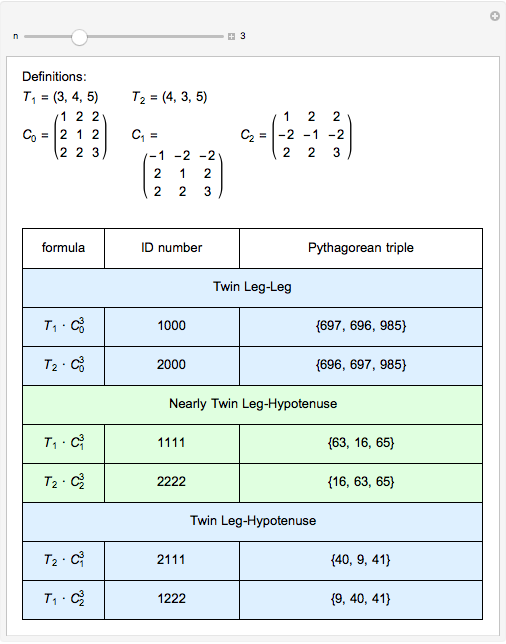
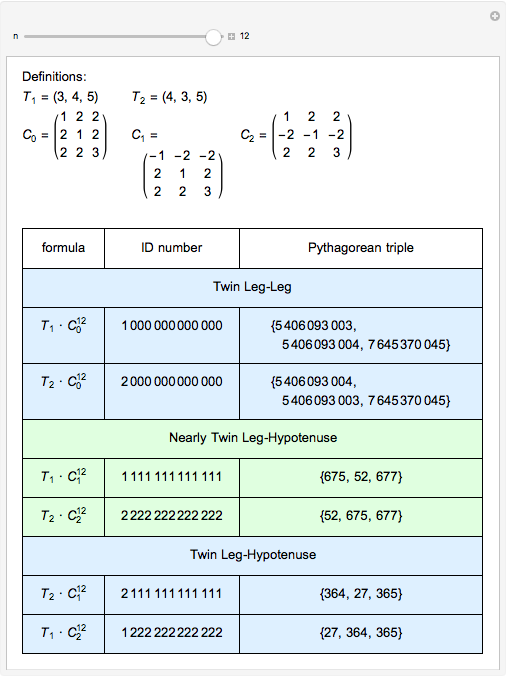
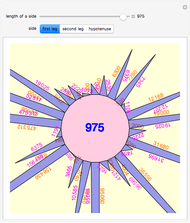
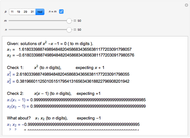
The (base 3) ID numbering system suggested by the author captures a concise description of the underlying formula for primitive Pythagorean triples. More than that, ID numbers with repeating last digits yield insight to other nearly twin and similar Pythagorean triples.
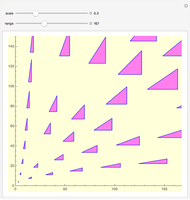
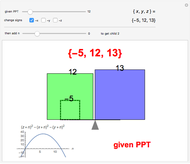
This method for generating twins also generates two classes of nearly twin leg-hypotenuse Pythagorean triples. Here are some additional examples.

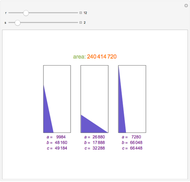
There are no nearly twin leg-leg Pythagorean triples, that is, where 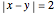 ; the next possible integer
; the next possible integer  after
after 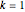 for
for 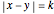 is
is  . Here are a few examples.
. Here are a few examples.

For a tool to look up and explore ID patterns, see the Demonstration, "Primitive Pythagorean Triples 3: Ordered Tree Graph".
Permanent Citation