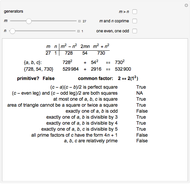
Primitive Pythagorean Triples on a Curvilinear Grid Defined by Euclid's Formula

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
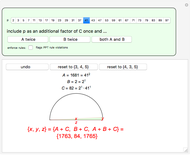
A primitive Pythagorean triple is a set of values 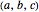 satisfying the Pythagorean theorem
satisfying the Pythagorean theorem 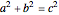 , with no common factors,
, with no common factors,  . The triples can be rewritten using Euclid's formula as
. The triples can be rewritten using Euclid's formula as 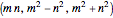 with
with  and
and  coprime and
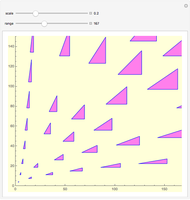
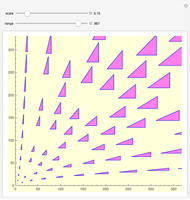
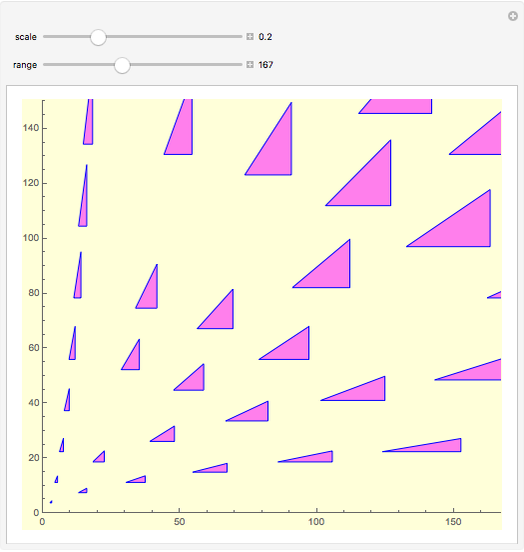
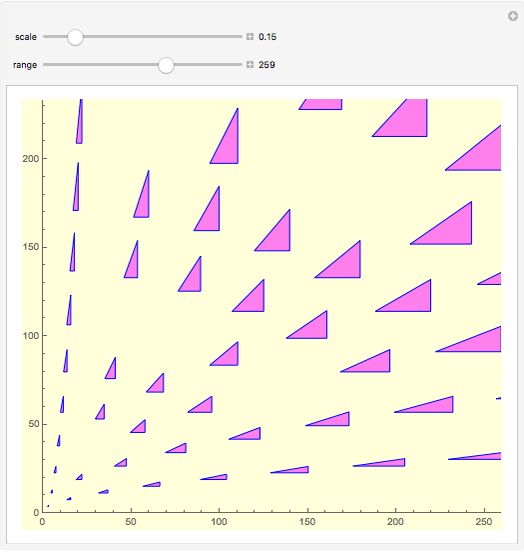
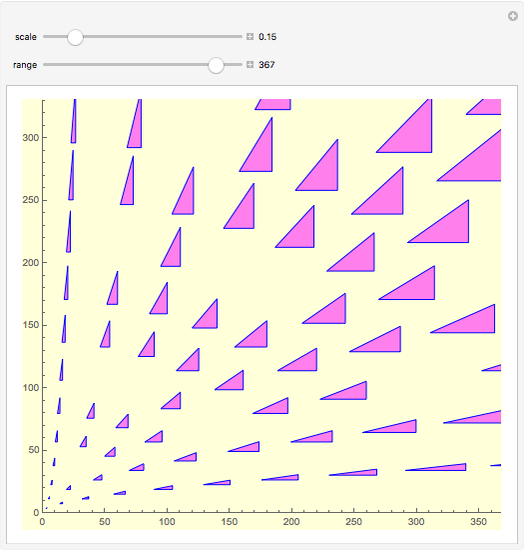
coprime and  odd to ensure that the triples are primitive. The primitive triples are represented by their corresponding triangles, scaled and translated to the intersection of the curves for each value
odd to ensure that the triples are primitive. The primitive triples are represented by their corresponding triangles, scaled and translated to the intersection of the curves for each value  ,
,  , in the centroid of the triangle. Empty intersections occur where the triple is not primitive.
, in the centroid of the triangle. Empty intersections occur where the triple is not primitive.
Contributed by: Enrique Zeleny (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
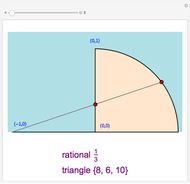
Let 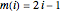 and
and 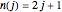 . Each blue curve is given parametrically by
. Each blue curve is given parametrically by 
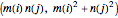 for fixed
for fixed 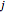 ; different values of
; different values of 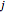 give different blue curves. The blue curves shown correspond to integer choices of
give different blue curves. The blue curves shown correspond to integer choices of 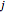 . Similarly, each red curve is given parametrically by
. Similarly, each red curve is given parametrically by 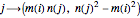 for fixed
for fixed  ; different values of
; different values of  give different red curves. The red curves shown correspond to integer choices of
give different red curves. The red curves shown correspond to integer choices of  .
.
Reference
[1] Wikipedia. "Pythagorean triple." (Sep 26, 2012) en.wikipedia.org/wiki/Pythagorean_triple.
Permanent Citation