Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

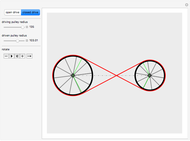
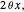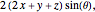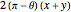Two Wheel Belt

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

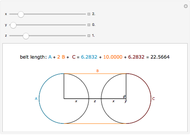
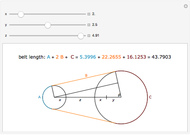
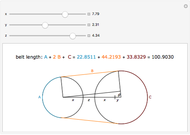
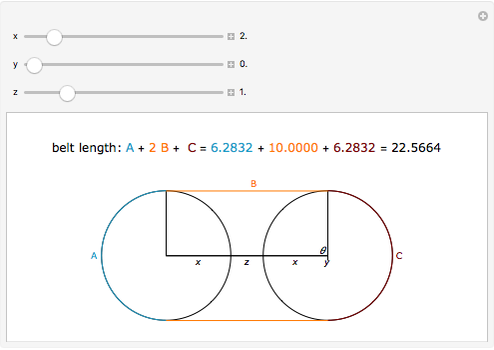
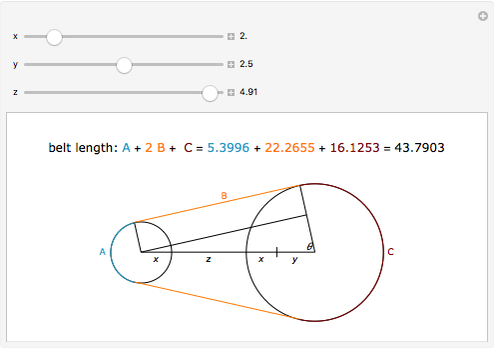
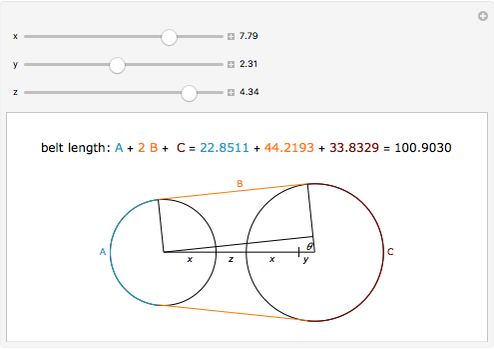
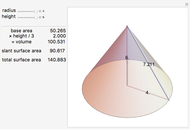
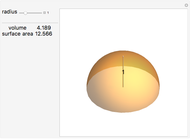
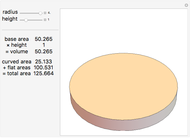
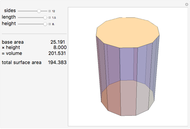
A classic trigonometry problem asks for the length of a belt wrapped around two wheels. The radii of the two wheels are and 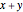. The wheels are units apart.

[more]

Let A and C be the two arcs of the belt and let B be one of the two segments joining the ends of the arcs. B is an exterior tangent to both circles. Then the lengths of A, B, and C are and .

[less]

Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send