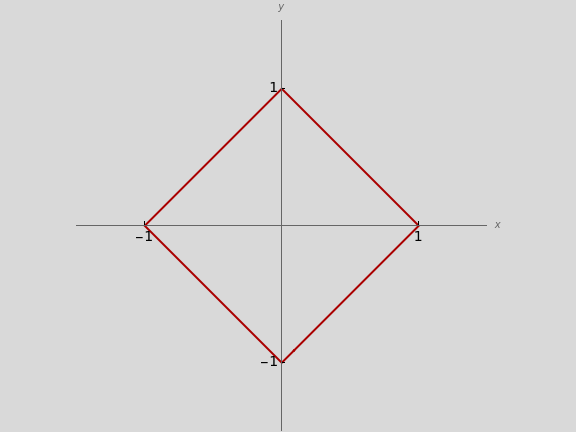
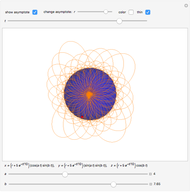
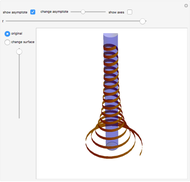
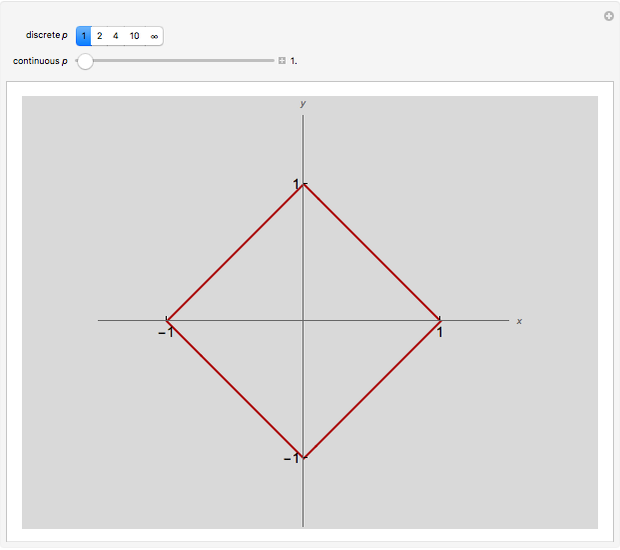
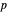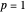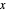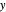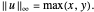Unit-Norm Vectors under Different p-Norms
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
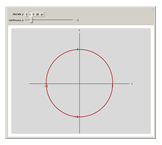
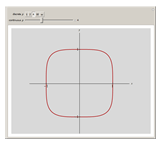
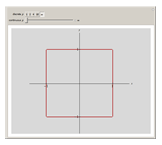
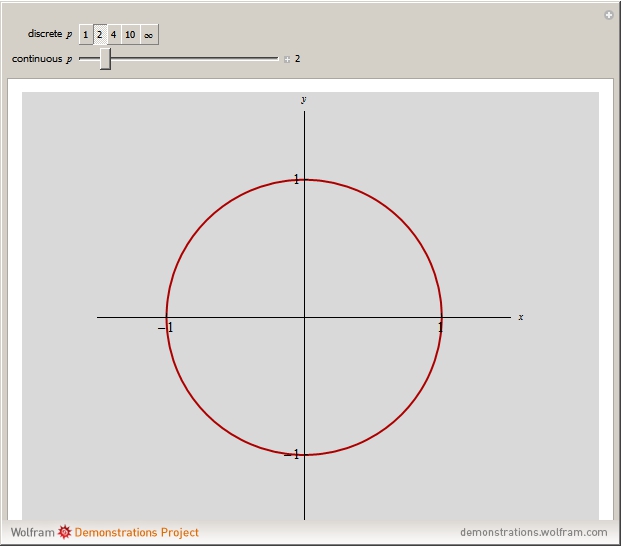
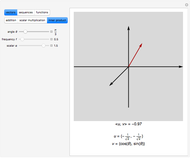
This Demonstration shows how unit-norm vectors look under different  -norms, which are standard norms for finite-dimensional spaces.
-norms, which are standard norms for finite-dimensional spaces.
Contributed by: Jelena Kovacevic (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Foundations of Signal Processing, Cambridge: Cambridge University Press, 2014. www.fourierandwavelets.org.
[2] Wikipedia. "Norm." (Jun 12, 2012) en.wikipedia.org/wiki/Norm_%28 mathematics %29.
Permanent Citation